Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Комплекс тоо, Ван Обелийн теорем
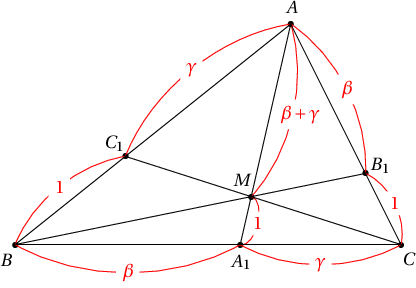
$A(0)$, $B(b)$, $C(c)$ ба $(AB,C_1)=\gamma$, $(AC,B_1)=\beta$ ба $M=BB_1\cap CC_1$ бол $$M=\dfrac{\gamma}{\beta+\gamma+1}B+\dfrac{\beta}{\beta+\gamma+1}C$$ болохыг батал.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Комплекс тоо ашиглан батлах.
Бодолт: $A=0$ ба $(AB,C_1)=\gamma$, $(BC,A_1)=\alpha$, $(CA,B_1)=\beta$ гэе. Тэгвэл $C_1=\dfrac{\gamma B}{1+\gamma}$, $B_1=\dfrac{\beta C}{1+\beta}$ ба
$$A_1=\dfrac{\gamma B+\beta C}{\beta+\gamma}$$
болно. $BB_1$, $CC_1$ шулуунуудын огтлолцол $M$ гэвэл
$$M=xC_1+(1-x)C=yB_1+(1-y)B$$
буюу
$$M=\dfrac{\gamma x}{1+\gamma}B+(1-x)C=\dfrac{\beta y}{1+\beta}C+(1-y)B$$
байна.
Иймд
$$\left\{\begin{array}{c}
\dfrac{\gamma x}{1+\gamma}=1-y\\
\dfrac{\beta y}{1+\beta}=1-x
\end{array}\right.\Leftrightarrow\left\{\begin{array}{c}
x=\dfrac{\gamma+1}{\beta+\gamma+1}\\
y=\dfrac{\beta+1}{\beta+\gamma+1}
\end{array}\right.$$
болно. Эндээс
\begin{align*}
M&=\dfrac{\gamma x}{1+\gamma}\cdot B+\dfrac{\beta y}{1+\beta}\cdot C\\
&=\dfrac{\gamma}{1+\gamma}\cdot\dfrac{\gamma+1}{\beta+\gamma+1}\cdot B+\dfrac{\beta}{1+\beta}\cdot\dfrac{\beta+1}{\beta+\gamma+1}\cdot C\\
&=\dfrac{\gamma}{\beta+\gamma+1}\cdot B+\dfrac{\beta}{\beta+\gamma+1}\cdot C
\end{align*}
болж батлагдав.