Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Комплекс тоог геометрт ашиглах
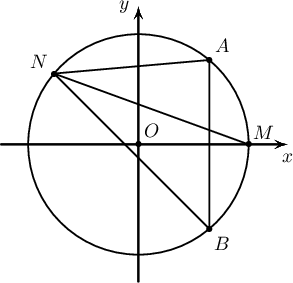
Тойргийн $AB$ нумын дундаж цэг $M$ болог. Энэ тойргийн дурын $N$ цэгийн хувьд $|AM^2-MN^2|=AN\cdot BN$ гэж батал.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
Бодолт: Өгөгдсөн тойргийн төв $O$ цэг хавтгайн эхийг авъя. $M$, $A$, $B$, $N$ цэгүүдийн координат $1$, $a$, $b$, $n$ байг. Тэгвэл $AB$ нумын дундаж цэг $M$ тул $a=\overline{b}$, $b=\overline{a\vphantom{b}}$ байна.
\begin{align*}
AN\cdot BN&=|a-n|\cdot |b-n|=|(a-n)(b-n)|\\
&=|a\overline{a}-na-n\overline{a}+n^2|=|n^2+1-n(a+\overline{a})|
\end{align*}
Нөгөө талаас
\begin{align*}
|AM^2-MN^2|&=|(a-1)(\overline{a}-1)-(n-1)(\overline{n}-1)|\\
&=|n+\overline{n}-a-\overline{a}|\cdot 1=|n+\overline{n}-a-\overline{a}|\cdot |n|\\
&=|n^2+1-n(a+\overline{a})|
\end{align*}
болж батлагдав.