Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ сорилго №1А, Бодлого №23
$AD$, $BC$ суурьтай $ABCD$ трапецийн $A$ ба $B$ оройн биссектрисүүдийн огтлолцлын цэг $K$ байв. $AB$ талын урт $20$ бол $ABK$ гурвалжныг багтаасан тойргийн радиусыг ол.
A.$10$ B.$2\sqrt{5}$ C.$5$ D.$25$ E.$20$
Бодлогын төрөл:Сонгох
Амжилтын хувь:27.88%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$\angle AKB=90^\circ$ болохыг харуул.
Бодолт: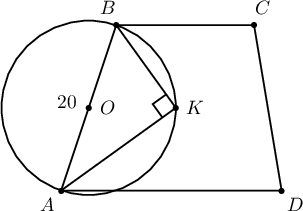
$$\angle A+\angle B=180^\circ, \angle BAK=\dfrac12\angle A, \angle ABK=\dfrac12\angle B$$
тул
$$\angle ABK+\angle BAK=90^\circ\Rightarrow \angle AKB=90^\circ$$
болно. Иймд $AB$ тал $ABK$ гурвалжныг багтаасан тойргийн диаметр тул $r=\dfrac{AB}{2}=\dfrac{20}{2}=10$ байна.