Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2020, B35
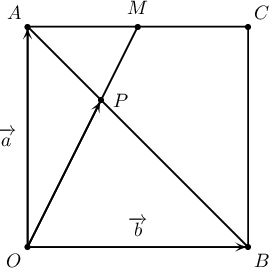
$OACB$ квадратын $AC$ талын дундаж цэг $M$ ба $AB$ диагональ $OM$ хэрчимтэй $P$ цэгт огтлолцдог. Хэрэв $\overrightarrow{OA}=\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{OB}=\overrightarrow{b\vphantom{OA}}$ бол $\overrightarrow{PM}$-ийг $\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{b\vphantom{OA}}$-ээр илэрхийл.
A.$\overrightarrow{a\vphantom{b}}+\overrightarrow{b}$ B.$\dfrac{2\overrightarrow{a\vphantom{b}}+\overrightarrow{b}}{2}$ C.$\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{3}$ D.$\dfrac{\overrightarrow{a\vphantom{b}}+2\overrightarrow{b}}{2}$ E.$\dfrac{\overrightarrow{2a\vphantom{b}}+\overrightarrow{b}}{3}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Бодолт байхгүй.
Сорилго
ЭЕШ 2020 A Вектор-Параллел, перпендикуляр нөхцөл Математик ЭЕШ Вектор ба координатын арга Аналитик геометрийн сорил. 11-р анги . А хувилбар