Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Мат 1.8
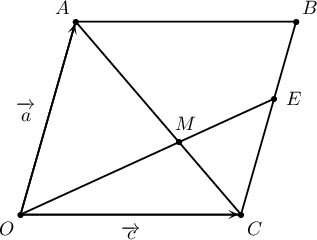
$OABC$ параллелограммын $BC$ талыг $BE:EC=2:3$ харьцаагаар хуваах цэгийг $E$ гэе. $AC$ диагональ $OE$ хэрчимтэй $M$ цэгт огтлолцдог байв. $\overrightarrow{OA}=\overrightarrow{a\vphantom{OA}}$, $\overrightarrow{OC}=\overrightarrow{c\vphantom{OC}}$ вектороор $\overrightarrow{OM}$ векторыг илэрхийлээрэй.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\triangle OMA\sim\triangle EMC$ ба $OA:CE=CB:CE=8:5=OM:ME$ тул
\begin{align*}
\overrightarrow{OM}&=\dfrac{8}{8+5}\overrightarrow{OE}=\dfrac{8}{13}\overrightarrow{OE}\\
&=\dfrac{8}{13}(\overrightarrow{OC}+\overrightarrow{CE})=\dfrac{8}{13}(\overrightarrow{c}+\dfrac{5}{8}\overrightarrow{a})\\
&=\dfrac{5}{13}\overrightarrow{a}+\dfrac{8}{13}\overrightarrow{c}
\end{align*}
байна.
Бодолт: