Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$M\left( \frac{1}{4};1 \right)$ цэгээс $y = x^{2} + \frac{1}{2}$ муруйн аль цэг хүртэлх зай хамгийн богино байх вэ?

$\Big(\dfrac12;\dfrac34\Big)$ B.

$\Big(1;\dfrac32\Big)$ C.

$\Big(-\dfrac12;\dfrac34\Big)$ D.

$\Big(-1;\dfrac32\Big)$ E.

$\Big(0;\dfrac12\Big)$

Бодлогын төрөл: Сонгох

Амжилтын хувь: 23.60%

Заавар: Уг цэгт татсан нормаль шулуун дээр

$M$ цэг оршино.

$y=f(x)$ функцийн графикийн

$(x_0;f(x_0))$ цэгт татсан нормаль шулууны тэгшитгэл:

$y=-\dfrac{1}{f^\prime(x_0)}(x-x_0)+f(x_0)$

Бодолт: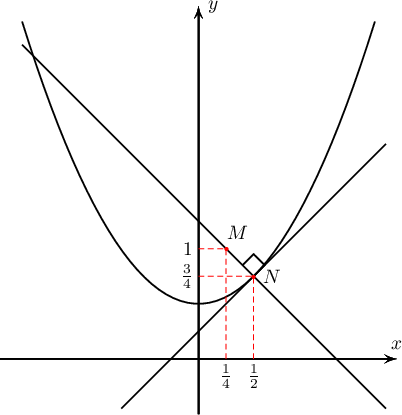

$y^\prime(x)=2x$ тул нормал шулууны тэгшитгэл нь:

$y=-\dfrac{1}{2x_0}(x-x_0)+x_0^2+\frac12$ ба энэ шулуун дээр

$M\left( \frac{1}{4};1 \right)$ цэг орших тул

$1=-\dfrac{1}{2x_0}\left(\frac14-x_0\right)+x_0^2+\frac12$ буюу

$8x_0^3-1=0\Rightarrow x_0=\dfrac12$ байна. Иймд

$y_0=\left(\dfrac12\right)^2+\dfrac12=\dfrac34$ буюу бидний олох цэгийн нь

$\Big(\dfrac12;\dfrac34\Big)$ байна.

Санамж: Энэ бодлогыг хариунаас бодох боломжтой. Мөн

$N\left(t,t^2+\frac12\right)$ гээд

$MN^2$ -ийн хамгийн бага утгыг олох аргаар бодож болно.