Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №2349
Хурц өнцөгт $ABC$ гурвалжинд $AD=5$, $CE=3$ байх өндрүүд татжээ. $AD$, $CE$ шулуунуудын хоорондох өнцөг нь $60^\circ$ бол $AC$ талын уртыг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\measuredangle B=120^\circ$. $ADB$, $CEB$ тэгш өнцөгт гурвалжнуудаас $BA$, $BC$ талуудын уртыг олоод косинусын теорем ашиглан $AC$-г ол.
Бодолт: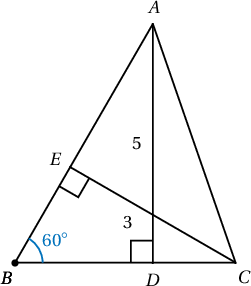 
$ADB$, $CEB$ тэгш өнцөгт гурвалжнуудаас $BA$, $BC$ талуудын уртыг олбол
$$BA=\dfrac{5}{\sin 60^\circ}=\dfrac{10\sqrt{3}}{3},\quad BC=\dfrac{3}{\sin 60^\circ}=2\sqrt{3}$$
болно. Косинусын теоремоор
\begin{align*}
AC^2&=BA^2+BC^2-2\cdot BA\cdot BC\cdot\cos60^\circ\\
&=\dfrac{100}{3}+12-20=\dfrac{76}{3}
\end{align*}
тул $AC=\sqrt{\dfrac{76}{3}}$ байна.
Сорилго
Косинусын теорем
Косинусын теорем тестийн хуулбар
Гурвалжныг бодох, зуны сургалт
06.4. Гурвалжныг бодох 1, зуны сургалт 2023