Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №2432
Адил хажуут гурвалжны суурийн урт $12$, хажуу талуудын урт $10$. Багтсан тойргийн хоёр хажууг шүргэх цэгүүдийн хоорондох зайг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Хэрвээ гурвалжны талууд $a,b,c$ ба $x,y,z$ нь харгалзан $A,B,C$ оройгуудаас багтсан тойрогт татсан шүргэгчүүдийн урт бол $x=\frac{b+c-a}{2}$, $y=\frac{a+c-b}{2}$, $z=\frac{c+b-a}{2}$ байдаг.
Бодолт: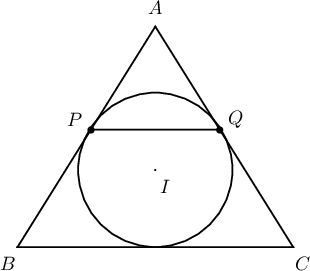 
Оройгоос хоёр хажууг шүргэх цэгүүд хүртэлх зай $AP=AQ=\dfrac{12+12-10}{2}=7$. $\triangle ABC\sim\triangle APQ$ тул
$$\dfrac{PQ}{BC}=\dfrac{AP}{AB}\Rightarrow PQ=\dfrac{5}{12}\cdot 10$$