Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №2508
Адил хажуут трапецийн сууриуд $a$, $b$ ба диагоналиуд перпендикуляр бол талбайг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: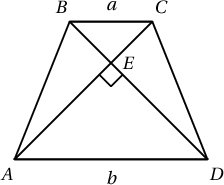 
Бодолт: Пифагорын теоремоор
$$BE^2+EC^2=BC^2\Rightarrow BE=\dfrac{a}{\sqrt{2}}$$
$$AE^2+ED^2=AD^2\Rightarrow ED=\dfrac{b}{\sqrt{2}}$$
тул $AC=BD=\dfrac{a+b}{\sqrt{2}}$. Иймд дөрвөн өнцөгтийн талбай
$$S=\dfrac{1}{2}AC\cdot BD\sin90^\circ=\dfrac{(a+b)^2}{4}$$
байна.