Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №2602
$ABCD$ параллелограммын $B$ мохоо өнцгийн биссектрис $AD$ талыг $F$ цэгт огтолно. $AB=12$, $AF:FD=4:3$ бол параллелограммын периметрийг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
Бодолт: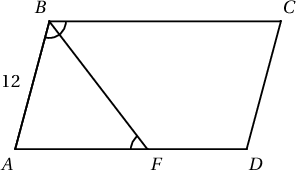 
Cолбисон өнцгүүд тул $\angle FBC=\angle BFA$ тэнцүү. Мөн $BF$ биссектрис тул $\angle FBC=\angle ABF$ тул $ABF$ гурвалжны суурийн өнцөгүүд тэнцүү болно. Иймд $\triangle ABF$ адил хажуут гурвалжин болно. Иймд $AF=AB=12$. $AF:FD=4:3$ тул $FD=\dfrac{3AF}{4}=9$ болно. Иймд $AD=AF+FD=12+9=21$ болов. Иймд параллелограммын периметр
$$2\cdot(12+21)=66$$
юм.