Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Квадратад багтсан зөв 8 өнцөгтийн талбай
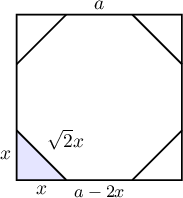
$a$ талтай квадратын өнцгүүдийг тайрч зөв найман өнцөгт үүсгэв. Энэ найман өнцөгтийн талбайг ол.
A.$\dfrac{3a^2}{4}$ B.$2(\sqrt2-1)a^2$ C.$\dfrac{\sqrt2a^2}{2}$ D.$(\sqrt2-1)a^2$ E.$(2-\sqrt2)a^2$
Бодлогын төрөл:Сонгох
Амжилтын хувь:57.14%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Квадратын оройгоос $x$ зайд оройг огтолсон гээд 8 өнцөгтийн талын уртыг 2 аргаар ол.
Бодолт:8 өнцөгтийн талын урт нь нэг талаас $a-2x$, нөгөө талаас $\sqrt2 x$ байна. Иймд
$$a-2x=\sqrt2x\Rightarrow x=\dfrac{a}{2+\sqrt2}$$
Найман өнцөгтийн талбай нь квадратын талбайгаас огтлогдсон гурвалжнуудын талбайг хасахад гарах тул
$$S=a^2-2x^2=a^2-\dfrac{2a^2}{(2+\sqrt2)^2}=\dfrac{(2+2\sqrt2)a^2}{3+2\sqrt2}=$$
$$=\dfrac{(2+2\sqrt2)(3-2\sqrt2)a^2}{(3+2\sqrt2)(3-2\sqrt2)}=2(\sqrt2-1)a^2$$
