Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Сорилго №2, 2019-2020
Пирамидын суурь нь $30^\circ$-ын хурц өнцөг бүхий 6 талтай ромбо байв. Хажуу талсуудын суурьтай үүсгэх хоёр талст өнцгүүд тэнцүү бөгөөд пирамидын хажуу гадаргуугийн талбай 36 бол хажуу талсуудын суурьтай үүсгэх хоёр талст өнцгийг градусаар илэрхийл.
A.$15^\circ$ B.$30^\circ$ C.$45^\circ$ D.$60^\circ$ E.$75^\circ$
Бодлогын төрөл:Сонгох
Амжилтын хувь:27.72%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Хоёр талст өнцгийг проекцийн талбайн харьцааг ашиглан олдог.
Бодолт: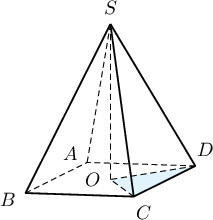
$$S_{COD}=\dfrac14S_{ABCD}=\dfrac14\cdot6^2\cdot\sin30^\circ=\dfrac{9}{2}$$
$$S_{CSD}=\dfrac14\cdot 36=9$$
байна. $CSD$-ийн суурь дээрх проекц нь $COD$ тул $\cos\alpha=\dfrac{S_{COD}}{S_{CSD}}=\dfrac12\Rightarrow\alpha=60^\circ$ байна. Энд $\alpha$ нь хажуу ирмэгийн суурийн хавтгайтай үүсгэх хоёр талст өнцөг юм.