Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2006 A №21
$3\cos^2x+\cos x\cdot\sin x=0.6$ тэгшитгэл $\Big[\dfrac{\pi}{2};\dfrac{3\pi}{2}\Big]$ завсар хэдэн шийдтэй вэ?
A.$8$ B.$6$ C.$4$ D.$3$ E.$2$
Бодлогын төрөл:Сонгох
Амжилтын хувь:24.17%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$$3\cos^2x+\cos x\cdot\sin x=0.6\Leftrightarrow 3\cos^2x+\cos x\cdot\sin x=0.6(\sin^2x+\cos^2x)$$
$$\Leftrightarrow 3+\tg x=0.6(\tg^2x+1)$$
тэгшитгэл болно. $\big[\frac{\pi}{2};\frac{3\pi}{2}\big]$ мужийн урт $\pi$ болохыг анхаар.
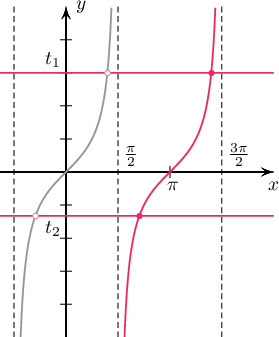
Бодолт:$3+\tg x=0.6(\tg^2x+1)$-д $t=\tg x$ орлуулга хийвэл $0.6t^2-t-2.4=0$ гэсэн $t_1=3$, $t_2=-\dfrac43$ гэсэн ялгаатай хоёр бодит шийдтэй тэгшитгэл болно. Тангес $\pi$ үетэй тул эдгээр 2 шийдэд харгалзах шийдүүд $\Big[\dfrac{\pi}{2};\dfrac{3\pi}{2}\Big]$ завсраас олдоно.
Сорилго
ЭЕШ 2006 A Тригонометр тэгшитгэл Илтгэгч, логарифм ба тригонометр тэгшитгэл, тэнцэтгэл биш 3 Тригонометр -1 тригонометрийн тэгшитгэл-2 Тригонометрийн тэгшитгэл Орлуулах арга. Нэгэн төрлийн тэгшитгэл бодох арга ЭЕШ 2006 A Тригонометрийн функц, зуны сургалт тригонометр тэгшитгэл 1 06.3. Тригонометрийн тэгшитгэл, тэнцэтгэл биш mo tegshitgel trigono tegshitgel