Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2006 A №29
$y=x^2-6x+K$ парабол $T(3;2)$ дээр оройтой тул $K=\fbox{ab}$ байна. $A(3;1)$; $B(5;3)$ цэгүүдийг дайрсан $y=x-\fbox{c}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $(AB)$ шулуунд хамгийн ойр цэг нь $M(\fbox{d}/2;\fbox{e}/4)$ болно. $AM$; $BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{f}$ байна.
ab = 11
c = 2
de = 79
f = 1
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 14.86%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $(x_0;y_0)$ координаттай цэг $y=f(x)$ тэгшитгэлтэй муруй дээр оршин байдаг бол $y_0=f(x_0)$ байна.
$(x_0;y_0)$ цэгээс $\ell\colon ax+by+c=0$ шулуун хүртэлх зай нь $$d(x_0;y_0)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$ байдаг.
$(x_0;y_0)$ цэгээс $\ell\colon ax+by+c=0$ шулуун хүртэлх зай нь $$d(x_0;y_0)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$ байдаг.
Бодолт: $(3;2)$ цэг парабол дээр орших тул $2=3^2-6\cdot 3+K\Rightarrow K=11$.
$A(3;1)$ цэг шулуун дээр орших тул $1=3-c\Rightarrow c=2$.
$M(s,t)$ гэвэл $t=s^2-6x+11$ байна. Цэгээс шулуун хүртэлх зайн томьёо ёсоор $$d(s)=\dfrac{|s-(s^2-6s+11)-2|}{\sqrt2}=\dfrac1{\sqrt2}(s^2-7s+13)$$ байна.
$$d(s)=\dfrac1{\sqrt2}(s^2-7s+13)=\dfrac1{\sqrt2}((s-3.5)^2+2.25)$$ тул $M(7/2,9/4)$ байна.
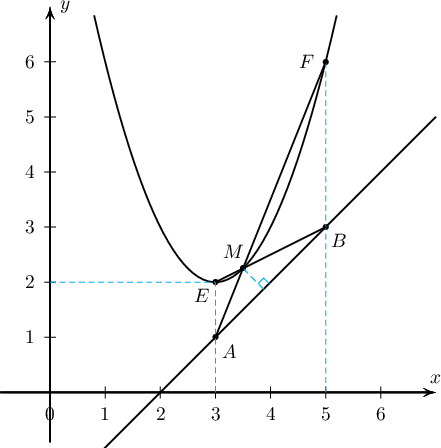Зургаас $AEFB$ нь трапец болох нь харагдаж байна ($AM$, $BM$ шулуунуудын тэгшитгэлийг бичээд параболтой огтолцох цэгүүд нь $E(3,2)$, $F(5,6)$ болохыг тогтоосноор баталж болно). Трапецийн диагоналуудаар үүсэх хоёр хажуу талд тулсан гурвалжнуудын талбай тэнцүү тул $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=1$ байна.
$A(3;1)$ цэг шулуун дээр орших тул $1=3-c\Rightarrow c=2$.
$M(s,t)$ гэвэл $t=s^2-6x+11$ байна. Цэгээс шулуун хүртэлх зайн томьёо ёсоор $$d(s)=\dfrac{|s-(s^2-6s+11)-2|}{\sqrt2}=\dfrac1{\sqrt2}(s^2-7s+13)$$ байна.
$$d(s)=\dfrac1{\sqrt2}(s^2-7s+13)=\dfrac1{\sqrt2}((s-3.5)^2+2.25)$$ тул $M(7/2,9/4)$ байна.