Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2006 C №29
$y=x^2-4x+K$ парабол $T(2;1)$ дээр оройтой тул $K=\fbox{a}$ байна. $A(2;0)$; $B(4;2)$ цэгүүдийг дайрсан $y=x-\fbox{b}$ тэгшитгэлтэй шулуун өгөгдөв. Парабол дээр орших $AB$ шулуунд хамгийн ойр цэг нь $M(\fbox{c}/2;\fbox{d}/4)$ болно. $AM; BM$ хэрчмүүдийн үргэлжлэлүүд нь параболыг харгалзан $F; E$ цэгүүдээр огтлох бол $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=\fbox{e}$ байна.
a = 5
b = 2
cd = 55
e = 1
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 17.09%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $(x_0;y_0)$ координаттай цэг $y=f(x)$ тэгшитгэлтэй муруй дээр оршин байдаг бол $y_0=f(x_0)$ байна.
$(x_0;y_0)$ цэгээс $\ell\colon ax+by+c=0$ шулуун хүртэлх зай нь $$d(x_0;y_0)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$ байдаг.
$(x_0;y_0)$ цэгээс $\ell\colon ax+by+c=0$ шулуун хүртэлх зай нь $$d(x_0;y_0)=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$ байдаг.
Бодолт: $(2;1)$ цэг парабол дээр орших тул $1=2^2-4\cdot 2+K\Rightarrow K=5$.
$A(2;0)$ цэг шулуун дээр орших тул $0=2-\fbox{b}\Rightarrow \fbox{b}=2$ буюу $AB$ шулууны тэгшитгэл $$y=x-2\Leftrightarrow x-y-2=0$$ $M(s,t)$ гэвэл $t=s^2-4s+5$ байна. Цэгээс шулуун хүртэлх зайн томьёо ёсоор \begin{align*} d(s)&=\dfrac{|s-(s^2-4s+5)-2|}{\sqrt2}\\ &=\dfrac{|-s^2+5s-7|}{\sqrt2}\\ &=\dfrac{|-(s-2.5)^2-0.75|}{\sqrt2}\\ &=\dfrac{(s-2.5)^2+0.75}{\sqrt2} \end{align*} байна. $d(s)$ нь хамгийн бага утгаа $s=2.5$ үед авах тул $$M(2.5,2.5^2-4\cdot 2.5+5)=M\left(\dfrac52;\dfrac{5}{4}\right)$$ байна.
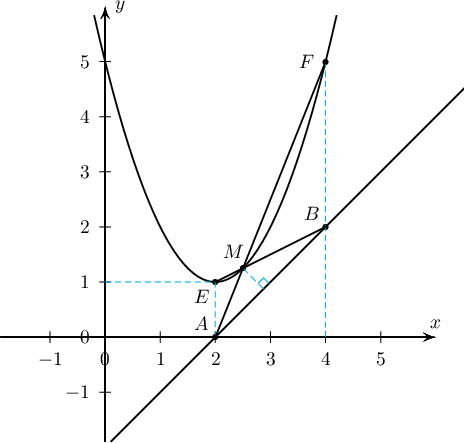 Зургаас $AEFB$ нь трапец болох нь харагдаж байна ($AM$, $BM$ шулуунуудын тэгшитгэлийг бичээд параболтой огтолцох цэгүүд нь $E(3,2)$, $F(5,6)$ болохыг тогтоосноор баталж болно). Трапецийн диагоналуудаар үүсэх хоёр хажуу талд тулсан гурвалжнуудын талбай тэнцүү тул $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=1$ байна.
Зургаас $AEFB$ нь трапец болох нь харагдаж байна ($AM$, $BM$ шулуунуудын тэгшитгэлийг бичээд параболтой огтолцох цэгүүд нь $E(3,2)$, $F(5,6)$ болохыг тогтоосноор баталж болно). Трапецийн диагоналуудаар үүсэх хоёр хажуу талд тулсан гурвалжнуудын талбай тэнцүү тул $\dfrac{S_{\triangle AMB}}{S_{\triangle FME}}=1$ байна.
Тайлбар: Ер нь 2006 оны тестийн бодлогууд харьцангуй хүнд байсан. Иймд бүх бодлогыг цагтаа амжиж бодох боломжгүй байлаа. Нөхөх тестийн бодлогуудыг бодолгүй зөвхөн сонгох тестийн бодлогуудаа бодоход 800 оноо авах боломжтой байв.
$A(2;0)$ цэг шулуун дээр орших тул $0=2-\fbox{b}\Rightarrow \fbox{b}=2$ буюу $AB$ шулууны тэгшитгэл $$y=x-2\Leftrightarrow x-y-2=0$$ $M(s,t)$ гэвэл $t=s^2-4s+5$ байна. Цэгээс шулуун хүртэлх зайн томьёо ёсоор \begin{align*} d(s)&=\dfrac{|s-(s^2-4s+5)-2|}{\sqrt2}\\ &=\dfrac{|-s^2+5s-7|}{\sqrt2}\\ &=\dfrac{|-(s-2.5)^2-0.75|}{\sqrt2}\\ &=\dfrac{(s-2.5)^2+0.75}{\sqrt2} \end{align*} байна. $d(s)$ нь хамгийн бага утгаа $s=2.5$ үед авах тул $$M(2.5,2.5^2-4\cdot 2.5+5)=M\left(\dfrac52;\dfrac{5}{4}\right)$$ байна.
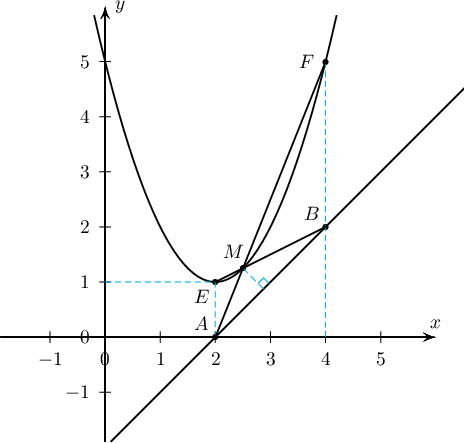
Тайлбар: Ер нь 2006 оны тестийн бодлогууд харьцангуй хүнд байсан. Иймд бүх бодлогыг цагтаа амжиж бодох боломжгүй байлаа. Нөхөх тестийн бодлогуудыг бодолгүй зөвхөн сонгох тестийн бодлогуудаа бодоход 800 оноо авах боломжтой байв.
Сорилго
ЭЕШ 2006 C
2006 оны ЭЕШ-ийн онцлох бодлогууд.
4.29
ЭЕШ 2006 C
Координатын арга А хэсэг тестийн хуулбар