Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2008 E №20
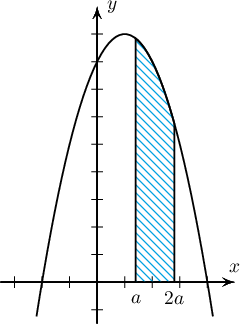
$x=a$, $x=2a$, $\left(0< a< 2\right)$, $y=0$, $y=8+2x-x^{2} $ шугамуудаар хүрээлэгдсэн дүрс $a$-ийн ямар утганд хамгийн их талбайтай байх вэ?
A.$1$ B.$\dfrac{-3+\sqrt{65} }{7} $ C.$\dfrac{9+\sqrt{753} }{14} $ D.$\dfrac{-9+\sqrt{753} }{14} $ E.$\dfrac{3+\sqrt{65} }{7} $
Бодлогын төрөл:Сонгох
Амжилтын хувь:33.84%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$\displaystyle f(a)=\int_a^{2a}(8+2x-x^2) \,\mathrm{d}x$ функц $a$-ийн ямар утганд хамгийн их утгатай байх вэ?
Бодолт:Хувьсах хилтэй интегралын уламжлал бодох томьёо ёсоор
\begin{align*}
f^\prime(a)&=\{8+2\cdot(2a)-(2a)^2\}\cdot 2-\{8+2\cdot a-a^2\}\cdot 1\\
&=(16+8a-8a^2)-(8+2a-a^2)=-7a^2+6a+8
\end{align*}
байна.
$$f^\prime(a)=0\Rightarrow a=\dfrac{-6\pm\sqrt{(-6)^2-4\cdot(-7)\cdot 8}}{2\cdot(-7)}=\dfrac{3\pm\sqrt{65}}{7}$$
болно. Түүнчлэн $f^{\prime\prime}(a)=-14a+6$ ба
$$-14\cdot\dfrac{3+\sqrt{65}}{7}+6=-2\sqrt{65}<0$$
тул $a=\dfrac{3+\sqrt{65}}{7}$ цэг дээр максимум утгаа авна.
Сорилго
ЭЕШ 2008 E Функцийн хязгаар, Уламжлал, Интеграл 3 сорилго №2 2019-2020 Интеграл Интеграл тестийн хуулбар Интеграл тестийн хуулбар Интеграл тестийн хуулбар тестийн хуулбар холимог тест 1.7 интеграл 2020-05-28 сорил мат 11 ЭЕШ 2008 E