Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2009 B1 №26
$ABCD$ пирамидын $ABD$, $BCD$, $CAD$ хажуу талсууд ижил талбайтай ба $AD$, $BD$, $CD$ ирмэгүүд дээр харгалзан $DA_1:DA=1:2$, $DB_1:DB=2:5$, $DC_1:DC=5:9$ байх $A_1, B_1, C_1$ цэгүүд авав. Тэгвэл $DA_1B_1C_1$ ба $DABC$ ($D$-орой) пирамидуудын хажуу гадаргуугийн талбайн харьцаа $\fbox{a}:\fbox{bc}$ (3 оноо), эзлэхүүний харьцаа $\fbox{d}:\fbox{e}$ байна. (4 оноо)
abc = 730
de = 19
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 9.07%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Дараах хоёр чанарыг ашиглая:
Баталгаа. $B$ ба $B'$ цэгүүдээс $H$ ба $H'$ өндрүүд буулгавал $\triangle ABH\sim \triangle AB'H'$ тул
$$\dfrac{B'H'}{BH}=\dfrac{AB'}{AB}=\dfrac{AB'}{AB'+B'B}=\dfrac{\alpha AB}{\alpha AB+(1-\alpha)AB}=\alpha$$
байна. Нөгөө талаас $S_{AB'C}=\dfrac12\cdot AC\cdot B'H'$, $S_{ABC}=\dfrac12\cdot AC\cdot BH$ тул
$$\dfrac{S_{AB'C}}{S_{ABC}}=\dfrac{B'H'}{BH}=\alpha$$
2 дахь хэсгийг үүнтэй аналогоор батална.
- $ABC$ гурвалжны $AB$ тал дээр $AB':B'B=\alpha:(1-\alpha)$ байхаар $B'$ цэг авахад $$\dfrac{S_{AB'C}}{S_{ABC}}=\alpha$$ байна.
- $ABCD$ пирамидын $AB$ ирмэг дээр $AB':B'B=\alpha:(1-\alpha)$ байхаар $B'$ цэг авахад $$\dfrac{V_{AB'CD}}{V_{ABCD}}=\alpha$$ байна.
Бодолт: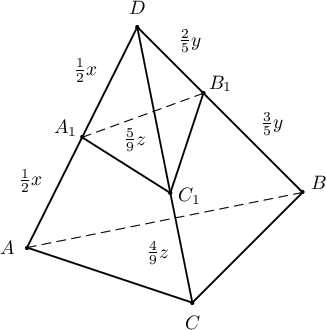 
Хажуу талсуудын талбайг $S$ гэвэл $$S_{DA_1B_1}=\dfrac12S_{DA_1B}=\dfrac12\cdot\dfrac25S=\dfrac15 S,$$ $$S_{DB_1C_1}=\dfrac25S_{DC_1B}=\dfrac25\cdot\dfrac59S=\dfrac29 S,$$ $$S_{DC_1A_1}=\dfrac59S_{DA_1C}=\dfrac59\cdot\dfrac12S=\dfrac5{18} S$$ байна. Иймд пирамидуудын хажуу гадаргуугийн харьцаа нь: $$\dfrac{\dfrac15S+\dfrac29S+\dfrac5{18}S}{3S}=\dfrac{7}{30}$$
2-р чанар ёсоор $\dfrac{V_{A_1BCD}}{V_{ABCD}}=\dfrac12$, $\dfrac{V_{A_1B_1CD}}{V_{A_1BCD}}=\dfrac25$, $\dfrac{V_{A_1B_1C_1D}}{V_{A_1B_1CD}}=\dfrac59$ байна. Эдгээрийг үржүүлбэл: $$\dfrac{V_{A_1B_1C_1D}}{V_{ABCD}}=\dfrac{1}{2}\cdot\dfrac{2}{5}\cdot\dfrac{5}{9}=\dfrac19$$ байна.
Хажуу талсуудын талбайг $S$ гэвэл $$S_{DA_1B_1}=\dfrac12S_{DA_1B}=\dfrac12\cdot\dfrac25S=\dfrac15 S,$$ $$S_{DB_1C_1}=\dfrac25S_{DC_1B}=\dfrac25\cdot\dfrac59S=\dfrac29 S,$$ $$S_{DC_1A_1}=\dfrac59S_{DA_1C}=\dfrac59\cdot\dfrac12S=\dfrac5{18} S$$ байна. Иймд пирамидуудын хажуу гадаргуугийн харьцаа нь: $$\dfrac{\dfrac15S+\dfrac29S+\dfrac5{18}S}{3S}=\dfrac{7}{30}$$
2-р чанар ёсоор $\dfrac{V_{A_1BCD}}{V_{ABCD}}=\dfrac12$, $\dfrac{V_{A_1B_1CD}}{V_{A_1BCD}}=\dfrac25$, $\dfrac{V_{A_1B_1C_1D}}{V_{A_1B_1CD}}=\dfrac59$ байна. Эдгээрийг үржүүлбэл: $$\dfrac{V_{A_1B_1C_1D}}{V_{ABCD}}=\dfrac{1}{2}\cdot\dfrac{2}{5}\cdot\dfrac{5}{9}=\dfrac19$$ байна.