Монгол Бодлогын Сан

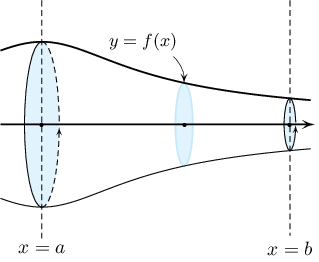
Заавар: $y=f(x)$ функцийн графикийн $a\le x\le b$ хэсгийг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $$V=\pi\int_a^b f^2(x)\,\mathrm{d}x$$ байдаг.

Бодолт: $$V=\pi\int\limits_0^{\sqrt3} \left(\dfrac{1}{\sqrt{1+x^2}}\right)^2\,\mathrm{d}x=\pi\int\limits_0^{\sqrt3} \dfrac{1}{1+x^2}\,\mathrm{d}x=\pi\big(\arctg x\Big|_0^{\sqrt3}\big)=\dfrac{\pi^2}{3}$$ байна.

$x=1$ цэгийг дарсан $Ox$ тэнхлэгт перпендикуляр $\alpha$ хавтгай ба $x=0$ цэгийг дарсан $Ox$ тэнхлэгт перпендикуляр хавтгайн хоорондох хэсгийн эзлэхүүн $$V_1=\pi\int\limits_0^1\dfrac{1}{1+x^2}\,\mathrm{d}x=\pi\big(\arctg x\Big|_0^1\big)=\dfrac{\pi^2}{4}$$ тул $$V_1:(V-V_1)=\dfrac{\pi^2}{4}:\left(\dfrac{\pi^2}{3}-\dfrac{\pi^2}{4}\right)=3:1$$ байна.

Энэ биетийн эзлэхүүнийг таллан хуваадаг, $\alpha$-тай паралель хавтгайг $x=a$ гэвэл $$\dfrac{V}{2}=\dfrac{\pi^2}{6}=\pi\int\limits_0^a \left(\dfrac{1}{\sqrt{1+x^2}}\right)^2\,\mathrm{d}x=\pi\big(\arctg x\Big|_0^a\big)=\pi\cdot\arctg a\Rightarrow a=\tg\dfrac{\pi}{6}=\dfrac{1}{\sqrt3}$$