Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2011 A №5
Параллел 2 хөвчийн урт 40 ба 48, хоорондох зай 22 бол тойргийн радиусыг ол. (Тойргийн төв хөвчүүдийн хооронд оршино гэж үзнэ.)
A.$25$ B.$33$ C.$\dfrac{142}{11}$ D.$\dfrac{315}{11}$ E.$\dfrac{355}{11}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:31.68%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: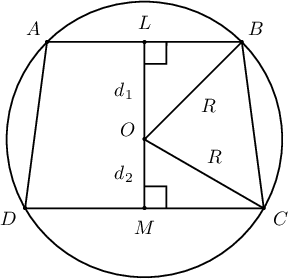
$d_1^2+LB^2=R^2$, $d_2^2+MC^2=R^2$, $d_1+d_2=LM$
Бодолт:Багтаасан тойргийн төвөөс сууриуд хүртэлх зайнуудыг $d_1$, $d_2$ гэе. Тэгвэл $d_1+d_2=22$, $d_1^2+20^2=R^2$, $d_2^2+24^2=R^2$ байна. Сүүлийн хоёр тэгшитгэлийг хасвал $$d_1^2-d_2^2=24^2-20^2\Leftrightarrow (d_1-d_2)(d_1+d_2)=176$$
болно. $d_1+d_2=22$ болохыг тооцвол $d_1-d_2=\dfrac{176}{22}=8$ байна. Энэ тэгшитгэлүүдийн системээс $d_1=\dfrac{22+8}{2}=15$, $d_2=\dfrac{22-8}{2}=7$ байна. Иймд $R^2=15^2+20^2=625\Rightarrow R=25$ байна.
Сорилго
ЭЕШ 2011 A 2016-05-21 ЭЕШ-2011 A alias 2020-03-09 сорил математик101 математик101 тестийн хуулбар математик101 тестийн хуулбар тестийн хуулбар Дунд сургуулийн геометр 99 99 тестийн хуулбар математик101 тестийн хуулбар тестийн хуулбар Тойрог, түүнтэй холбоотой бодлогууд ЭЕШ 2011 A тестийн хуулбар 2021-05-10 сорил 2021-05-10 сорил 2021-05-11 сорил 2021-05-11 сорил тестийн хуулбар Багтсан ба багтаасан тойрог