Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2011 A №24
$A(1;1)$, $B(4;1)$, $C(4;5)$ цэгүүд гурвалжны оройнууд бол өнцгүүдийн косинусыг ол. $\overrightarrow{AB}(3;0)$, $\overrightarrow{AC}(3;4)$, $\overrightarrow{BC}(0;4)$ векторын уртыг олбол $|\overrightarrow{AB}|=\fbox{a}$, $|\overrightarrow{BC}|=\fbox{b}$, $|\overrightarrow{AC}|=\fbox{c}$. Хоёр векторын скаляр үржвэрийг олох томъёоноос $\cos\angle A=\dfrac{\fbox{d}}{\fbox{e}}; \cos\angle B=\fbox{f}; \cos\angle C=\dfrac{\fbox{g}}{\fbox{h}}$.
abc =345
de =35
f =0
gh =45
Бодлогын төрөл:Нөхөх
Амжилтын хувь:12.77%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Цэгүүдийг координатын хавтгайд тэмдэглэ.
Бодолт: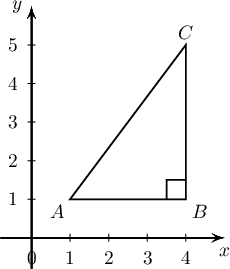
Зургаас харахад $AB=4-1=3$, $BC=5-1=4$ ба $\angle B=90^\circ$ тул $AC=\sqrt{3^2+4^2}=5$ байна. Түүнчлэн
$\cos\angle A=\dfrac{AB}{AC}=\dfrac{3}{5}$, $\cos\angle B=\cos 90^\circ=0$, $\cos\angle C=\dfrac{BC}{AC}=\dfrac{4}{5}$.