Монгол Бодлогын Сан

Заавар: $f(x)=x^2+bx+c$ байг. $f(x)=0$ тэгшитгэл $x_1< x_2< p$ гэсэн 2 бодит шийдтэй байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $D>0$, $x_0=-\dfrac{b}{2}< p$ ба $f(p)>0$ байдаг.

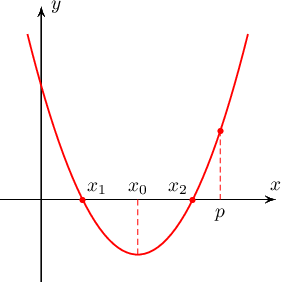
Бодолт: Квадрат тэгшитгэл $2$-оос бага ялгаатай 2 шийдтэй байх нөхцлийг бичвэл $$\left\{\begin{array}{c}D=(p-2)^2-4\cdot1\cdot [-(p-2)]>0\\ x_0=\dfrac{p-2}{2}< 2\\ 2^2-(p-2)\cdot 2+p-2>0 \end{array}\right.\Leftrightarrow$$ $$\left\{\begin{array}{c}D=p^2-8p+12>0\\ x_0=\dfrac{p-2}{2}< 2\\ 6-p>0 \end{array}\right.\Leftrightarrow\left\{\begin{array}{c}\left[\begin{array}{c}p<2\\ p>6\end{array}\right.\\ p<6 \end{array}\right.$$ тул системийн шийд $p$