Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2012 A №20
Адил хажуут трапецийн сууриуд 8 ба 16 нэгж урттай бөгөөд диагональ нь суурийн өнцгөө таллан хуваадаг бол трапецийн талбайг ол.
A.$48\sqrt3$ B.$56\sqrt2$ C.$72$ D.$72\sqrt3$ E.$80$
Бодлогын төрөл:Сонгох
Амжилтын хувь:40.46%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
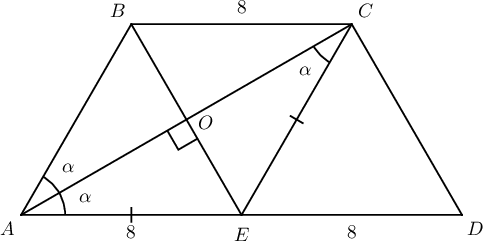
Заавар:$BC=8$, $AD=16$ ба $E$ нь $AD$ талын дундаж цэг бол $ABCE$ нь ромбо байна.
Талын урт нь $a$-тай тэнцүү зөв гурвалжны талбайг $S=\dfrac{a^2\sqrt3}{4}$ томьёогоор олдог.
Талын урт нь $a$-тай тэнцүү зөв гурвалжны талбайг $S=\dfrac{a^2\sqrt3}{4}$ томьёогоор олдог.
Бодолт:Солибосон өнцгүүд тул $\angle ACE=\angle CAB$ ба $AC$ биссектрис тул $\angle CAB=\angle EAC$ байна. Иймд $\triangle ACE$ нь $AE=EC$ байх адил хажуут гурвалжин болно. Иймд $EC=AB=8$, $EB=8$ болно.
$\triangle ABE$, $\triangle EBC$, $\triangle CDE$ нь бүгд 8 талбай адил талт гурвалжнууд тул $$S_{ABCD}=3\cdot\dfrac{8^2\sqrt3}{4}=48\sqrt3$$ байна.
$\triangle ABE$, $\triangle EBC$, $\triangle CDE$ нь бүгд 8 талбай адил талт гурвалжнууд тул $$S_{ABCD}=3\cdot\dfrac{8^2\sqrt3}{4}=48\sqrt3$$ байна.
Сорилго
ЭЕШ 2012 A 2016-05-14 ЭЕШ-2012 A alias Хавтгайн геометр 2020 он 2 сарын 20 Хувилбар 2 2020-04-06 soril 2020-04-07 Сорил Дунд сургуулийн геометр ЭЕШ 2012 A тестийн хуулбар ДӨРВӨН ӨНЦӨГТ ЭЕШ 2012 A тестийн хуулбар 9-r Songon