Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2014 A №37
Зургаас дараах функцийн $$f(x)=\left\{\begin{array}{lll}\fbox{ab}, & x\le-2 & (2\text{ оноо)}\\ \fbox{c}\cdot x+\fbox{d}, & -2< x\le -1 & (2\text{ оноо)}\\ \fbox{e}\cdot x+\fbox{f}, & -1< x\le 0 & (2\text{ оноо)}\\ \fbox{g}, & x>0 & (1\text{ оноо)}\end{array}\right.$$
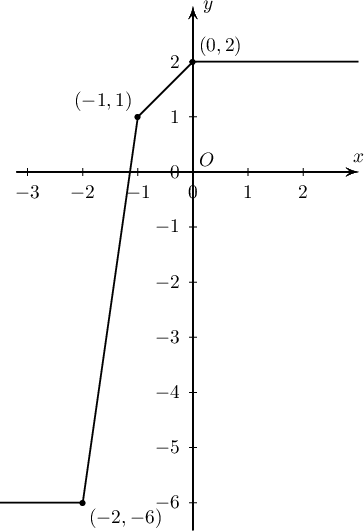
ab =-6
cd =78
ef =12
g =2
Бодлогын төрөл:Нөхөх
Амжилтын хувь:23.14%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$(x_1;y_1), (x_2;y_2)$ цэгүүдийг дайрсан шулууны тэгшитгэл:
- $x_1\neq x_2, y_1\neq y_2$ үед $\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}$
- $x_1=x_2$ бол $x=x_1$
- $y_1=y_2$ бол $y=y_1$
Бодолт:
- $x\le -2$ үед $(-3;-6), (-2;-6)$ цэгүүдийг дайрсан шулуун буюу $y=-6$ тул $\fbox{ab}=-6$;
- $-2< x\le -1$ үед $(-2;-6), (-1;1)$ цэгүүдийг дайрсан шулуун буюу $$\dfrac{x+2}{-1+2}=\dfrac{y+6}{1+6}\Leftrightarrow y=7x+8$$ тул $\fbox{c}=7, \fbox{d}=8$,
- $-1< x\le 0$ үед $(-1;1), (0;2)$ цэгүүдийг дайрсан шулуун буюу $$\dfrac{x+1}{0+1}=\dfrac{y-1}{2-1}\Leftrightarrow y=x+2$$ тул $\fbox{e}=1, \fbox{f}=2$,
- $0< x$ үед $(0;2), (1;2)$ цэгүүдийг дайрсан шулуун буюу $y=2$ тул $\fbox{g}=2$ болно.
Сорилго
ЭЕШ 2014 A 2017-03-07 ЭЕШ-2014 A alias 4.30 2020-11-25 сорил ЭЕШ 2014 A тест ЭЕШ 2014 A тест ААТТШ ЭЕШ 2014 A тест тестийн хуулбар 2024-03-16 сургуулийн сорил 2024-03-16 сургуулийн сорил тестийн хуулбар 2024-05-30