Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тригонометр тэнцэтгэл биш
$\sin^4x+\cos^4x< \dfrac34$ тэнцэтгэл бишийн шийд $$\dfrac{\pi k}{2}+\dfrac{\pi}{\fbox{a}}< x< \dfrac{\fbox{b}\pi}{\fbox{c}}+\dfrac{\pi k}{2},~k\in\mathbb Z$$ байна. Энэ шийдэд агуулагдахгүй хамгийн бага эерэг бүхэл тоо $x=\fbox{d}$, хамгийн их сөрөг бүхэл тоо $x=-\fbox{e}$ болно.
abc = 838
d = 3
e = 3
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 36.17%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Зэргийг бууруул.
Бодолт: \begin{gather*}
\sin^4x+\cos^4x=(\sin^2x+\cos^2x)^2-2\sin^2x\cos^2x=\\
=1-\frac12\sin^22x=1-\frac12\cdot\frac{1-\cos4x}{2}=\frac{3+\cos 4x}{4}
\end{gather*}
тул $\sin^4x+\cos^4x< \frac34\Leftrightarrow \frac{3+\cos4x}{4}< \frac34\Leftrightarrow \cos4x< 0$.
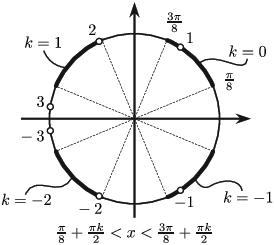
Иймд $\frac{\pi}{2}+2\pi k< 4x< \frac{3\pi}{2}+2\pi k$ буюу $\frac{\pi}{8}+\frac{\pi k}{2}< x< \frac{3\pi}{8}+\frac{\pi k}{2}$.
$k=0$ үед $\frac{\pi}{8}< 1< \frac{3\pi}{8}$, $k=1$ үед $1.96\approx\frac{5\pi}{8}< 2< \frac{7\pi}{8}$ тул 1 ба 2 нь шийд болно. 3 нь шийд биш болохыг харахад төвөгтэй биш (зураг үз). Иймд шийдэд орохгүй хамгийн бага эерэг бүхэл тоо нь 3 байна.
Мөн төстэй шалтгаанаар шийдэд орохгүй хамгийн их сөрөг бүхэл тоо нь $-3$ байна.
Иймд $\frac{\pi}{2}+2\pi k< 4x< \frac{3\pi}{2}+2\pi k$ буюу $\frac{\pi}{8}+\frac{\pi k}{2}< x< \frac{3\pi}{8}+\frac{\pi k}{2}$.
$k=0$ үед $\frac{\pi}{8}< 1< \frac{3\pi}{8}$, $k=1$ үед $1.96\approx\frac{5\pi}{8}< 2< \frac{7\pi}{8}$ тул 1 ба 2 нь шийд болно. 3 нь шийд биш болохыг харахад төвөгтэй биш (зураг үз). Иймд шийдэд орохгүй хамгийн бага эерэг бүхэл тоо нь 3 байна.
Мөн төстэй шалтгаанаар шийдэд орохгүй хамгийн их сөрөг бүхэл тоо нь $-3$ байна.