Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Бодлого №4700
$0< x< \pi, x\ne\dfrac{\pi}{2}$ бол $2\sin x-2\cos x+\tg x-1=0$ тэгшитгэл бод.
A.шийдгүй B.$x=\dfrac{\pi}{4}, \dfrac{2\pi}{3}$ C.$x=\dfrac{\pi}{3}, \dfrac{2\pi}{3}$ D.$x=\dfrac{\pi}{4}$ E.$x=\dfrac{\pi}{6},\dfrac{2\pi}{3}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:57.89%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Үржигдэхүүнд задлах аргаар бод.
Бодолт: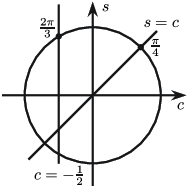
$0< x< \pi, x\ne\frac{\pi}{2}$ тул $\cos x\ne0$ байна. $$2\sin x-2\cos x+\dfrac{\sin x}{\cos x}-1=0\Leftrightarrow$$ $$\Leftrightarrow 2(\sin x-\cos x)\cos x+(\sin x-\cos x)=0$$ буюу $$(2\cos x+1)(\sin x-\cos x)=0.$$ Иймд $\cos x=-\dfrac12$ эсвэл $\sin x=\cos x$ байна. $0< x< \pi$ тул эхний тэгшитгэлээс $x=\dfrac{2\pi}{3}$, хоёр дахь тэгшитгэлээс $x=\dfrac{\pi}{4}$ шийд гарна.
$0< x< \pi, x\ne\frac{\pi}{2}$ тул $\cos x\ne0$ байна. $$2\sin x-2\cos x+\dfrac{\sin x}{\cos x}-1=0\Leftrightarrow$$ $$\Leftrightarrow 2(\sin x-\cos x)\cos x+(\sin x-\cos x)=0$$ буюу $$(2\cos x+1)(\sin x-\cos x)=0.$$ Иймд $\cos x=-\dfrac12$ эсвэл $\sin x=\cos x$ байна. $0< x< \pi$ тул эхний тэгшитгэлээс $x=\dfrac{2\pi}{3}$, хоёр дахь тэгшитгэлээс $x=\dfrac{\pi}{4}$ шийд гарна.
Сорилго
ЭЕШ математик №04 hw-55-2016-04-22 Тригонометрийн тэгшитгэл. Үржигдэхүүн болгон задлах арга Тригонометрийн тэгшитгэл Нийлбэрийг үржвэрт хувиргах томъёо хэрэглэх