Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Гурвалжин ашиглан 4 өнцөгт бодох
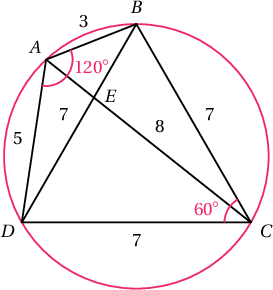
$O$ тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн талууд $AB=3$, $BC=7$, $CD=7$, $DA=5$ байв. $ABD$ ба $BDC$ гурвалжнуудаас косинусын теорем бичвэл $\angle C=\fbox{ab}, BD=\fbox{c}$ болно. Тойрогт багтсан дөрвөн өнцөгтийн чанараар $AC=\fbox{d}$ болно. $ABCD$ дөрвөн өнцөгтийн талбай $\fbox{ef}\sqrt{\fbox{g}}$ байна.
$O$ тойргийн радиуc $\dfrac{\fbox{h}\sqrt{\fbox{i}}}{\fbox{j}}$ байна. $ABD$ гурвалжинд багтсан тойргийн радиус $\dfrac{\sqrt{\fbox{k}}}{\fbox{l}}$ байна. $ABCD$ дөрвөн өнцөгтийн диагоналиудын огтлолцолын цэг $E$ бол $\sin\angle AEB=\dfrac{\fbox{m}\sqrt{\fbox{n}}}{\fbox{o}}$ байна.
ab = 60
c = 7
d = 8
efg = 163
hij = 733
kl = 32
mno = 437
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 25.62%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Синусын теорем, косинусын теорем болон дараах томьёонуудыг ашиглан бодоорой.
Гурвалжны хагас периметр, багтаасан ба багтсан тойргийн радиус: $$p=\dfrac{a+b+c}{2},\ R=\dfrac{abc}{4S},\ r=\dfrac{S}{p}$$
Гурвалжны талбай: $$S=\frac12 ab\sin\gamma=\frac12 ac\sin\beta=\frac12 bc\sin\alpha$$
Гурвалжны хагас периметр, багтаасан ба багтсан тойргийн радиус: $$p=\dfrac{a+b+c}{2},\ R=\dfrac{abc}{4S},\ r=\dfrac{S}{p}$$
Гурвалжны талбай: $$S=\frac12 ab\sin\gamma=\frac12 ac\sin\beta=\frac12 bc\sin\alpha$$
Бодолт: $ABD$ ба $BDC$ гурвалжнуудад косинусын теорем бичвэл
$$BD^2=5^2+3^2-2\cdot5\cdot3\cdot\cos\angle A=7^2+7^2-2\cdot7\cdot7\cdot\cos\angle C.$$
$\angle A+\angle C=180^\circ$, $\cos(180^\circ-\alpha)=-\cos\alpha$ тул
$$30\cos\angle C+98\cos\angle C=98-34\Rightarrow\cos\angle C=\frac12\Rightarrow\angle C=60^\circ, BD=7$$
болно. Тойрогт багтсан дөрвөн өнцөгтийн чанараар (Птолемейн теорем) $$AC\cdot BD=AB\cdot CD+AD\cdot BC$$ буюу $$AC\cdot 7=3\cdot 7+5\cdot 7.$$ Иймд $AC=8$ болно.
 $ABCD$ дөрвөн өнцөгтийн талбай $$S=S_{ABD}+S_{BCD}=\dfrac12\cdot7\cdot7\sin60^\circ+\dfrac12\cdot3\cdot5\cdot\sin120^\circ=16\sqrt{3}$$ байна. $O$ тойргийн радуис $\dfrac{BD}{2\sin60^\circ}=\dfrac{7\sqrt3}{3}$ байна. $ABD$ гурвалжинд багтсан тойргийн радиус $$\dfrac{2S_{ABD}}{AB+BD+DA}=\dfrac{AB\cdot AD\cdot\sin120^\circ}{3+7+5}=\dfrac{\dfrac{15\sqrt3}{2}}{15}=\dfrac{\sqrt3}{2}$$ байна. $ABCD$ дөрвөн өнцөгтийн диагоналиудын огтолцолын цэг $E$ бол $S=\dfrac12 AC\cdot BD\cdot\sin\angle AEB$ буюу $16\sqrt3=\dfrac12\cdot 8\cdot 7\cdot\sin\angle AEB$. Эндээс $\sin\angle AEB=\dfrac{4\sqrt{3}}{7}$ байна.
$ABCD$ дөрвөн өнцөгтийн талбай $$S=S_{ABD}+S_{BCD}=\dfrac12\cdot7\cdot7\sin60^\circ+\dfrac12\cdot3\cdot5\cdot\sin120^\circ=16\sqrt{3}$$ байна. $O$ тойргийн радуис $\dfrac{BD}{2\sin60^\circ}=\dfrac{7\sqrt3}{3}$ байна. $ABD$ гурвалжинд багтсан тойргийн радиус $$\dfrac{2S_{ABD}}{AB+BD+DA}=\dfrac{AB\cdot AD\cdot\sin120^\circ}{3+7+5}=\dfrac{\dfrac{15\sqrt3}{2}}{15}=\dfrac{\sqrt3}{2}$$ байна. $ABCD$ дөрвөн өнцөгтийн диагоналиудын огтолцолын цэг $E$ бол $S=\dfrac12 AC\cdot BD\cdot\sin\angle AEB$ буюу $16\sqrt3=\dfrac12\cdot 8\cdot 7\cdot\sin\angle AEB$. Эндээс $\sin\angle AEB=\dfrac{4\sqrt{3}}{7}$ байна.

Сорилго
ЭЕШ математик №04
2016-04-15
Косинусын теорем
Геометр сэдвийн давтлага 2
Косинусын теорем
Косинусын теорем тестийн хуулбар
Синус, косинусын теорем
Геометр сэдвийн давтлага 2 тестийн хуулбар