Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$f(x)=ax^3+3ax^2+b, (-1\le x\le 2)$ функцийн хамгийн их, хамгийн бага утга нь харгалзан $10,-10$ бол $|a+b|=?$

A. 10 B. 9 C. 8 D. 6 E. 11

Бодлогын төрөл: Сонгох

Амжилтын хувь: 4.88%

Заавар:

$a$ ,

$b$ -ийн тэмдэгийг нэгэн зэрэг өөрчлөхөд хамгийн их, хамгийн бага утга нь

$10$ ,

$-10$ хэвээрээ бөгөөд

$|a+b|$ өөрчлөгдөхгүй. Иймд

$a>0$ гэж үзээд бодож болно.

Бодолт: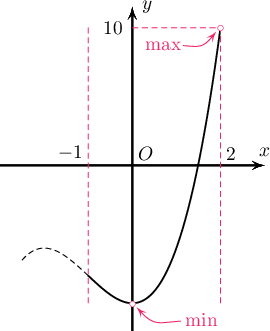

$f^\prime(x)=3ax^2+6ax=0\Rightarrow x_1=-2$ ,

$x_2=0$ . Тэгвэл

$x=0$ цэг дээр хамгийн бага утгатай. Иймд

$f(0)=b=-10$ . Түүнчлэн

$x=-1$ ,

$x=2$ -ийн аль нэг дээр хамгийн их утгатай байна.

$f(-1)=2a-10$ ,

$f(2)=20a-10$ ба

$a>0$ тул

$f(2)>f(-1)$ буюу

$x=2$ үед хамгийн их утгатай. Иймд

$20a-10=10\Rightarrow a=1$ тул

$|a+b|=|1-10|=9$ .