Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Модультай тэнцэтгэл биш
$|2x+3|\le 4+|x|$ тэнцэтгэл бишийн шийдийн интервалын уртыг ол.
A. 6
B. 7
C. 8
D. 9
E. 10
Бодлогын төрөл: Сонгох
Амжилтын хувь: 20.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $[a,b]$; $[a,b[$; $]a,b]$; $]a,b[$ интервалуудын урт $b-a$ юм.
Бодолт: $2x+3=0\Rightarrow x=-1.5$ тул $x< -1.5$; $-1.5\le x< 0$; $0\le x$ гэсэн 3 мужид тэнцэтгэл бишийг бодъё.
а) $x< -1.5$ үед $2x+3< 0, x< 0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow -2x-3\le 4-x\Leftrightarrow -7\le x.$$ Иймд энэ мужид шийд нь $[-7;-1.5[$.
б) $-1.5\le x< 0$ үед $2x+3\ge 0, x< 0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow 2x+3\le 4-x\Leftrightarrow x< \frac13.$$ Иймд шийд нь муж бүхлээрээ $[-1.5;0[$.
в) $0\le x$ үед $2x+3\ge 0, x\ge0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow 2x+3\le 4+x\Leftrightarrow x\le 1$$ буюу байна. Иймд энэ мужид шийд нь $[0;1]$.
Шийдүүдээ нэгтгэвэл $[-7;1]$ байна. Иймд урт нь $|1-(-7)|=8$.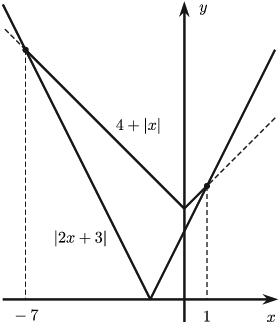
а) $x< -1.5$ үед $2x+3< 0, x< 0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow -2x-3\le 4-x\Leftrightarrow -7\le x.$$ Иймд энэ мужид шийд нь $[-7;-1.5[$.
б) $-1.5\le x< 0$ үед $2x+3\ge 0, x< 0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow 2x+3\le 4-x\Leftrightarrow x< \frac13.$$ Иймд шийд нь муж бүхлээрээ $[-1.5;0[$.
в) $0\le x$ үед $2x+3\ge 0, x\ge0$ тул $$|2x+3|\le 4+|x|\Leftrightarrow 2x+3\le 4+x\Leftrightarrow x\le 1$$ буюу байна. Иймд энэ мужид шийд нь $[0;1]$.
Шийдүүдээ нэгтгэвэл $[-7;1]$ байна. Иймд урт нь $|1-(-7)|=8$.