Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Параллелограмын талуудын урт
$O$ нь $ABCD$ параллелограммын диагоналиудын огтлолцолын цэг байг. Параллелограммын периметр нь 12-той тэнцүү ба $BOC$ ба $COD$ гурвалжны периметрүүдийн ялгавар 2-той тэнцүү бол параллелограммын талуудын уртыг ол.
A.2 ба 4 B.5 ба 7 C.4 ба 8 D.3 ба 6 E.1 ба 5
Бодлогын төрөл:Сонгох
Амжилтын хувь:50.00%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Параллелограммын диагоналиуд огтлолцлын цэгээрээ таллан хуваагддаг.
Бодолт: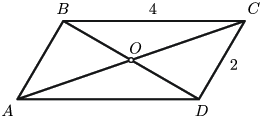
$BO=OD$ тул
\begin{gather}
(BO+OC+BC)-(OC+OD+CD)=BC-CD=2\\
AB+BC+CD+DA=2(BC+CD)=12
\end{gather} Эндээс $BC=4$, $CD=2$ болов.