Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Модультай рационал тэнцэтгэл биш
$\dfrac{9}{|x-5|-3}\leq|2-x|$ тэнцэтгэл бишийн бүх шийдийг ол.
A. $[-1;2]\cup[5-3\sqrt{2};5]$
B. $[-1;2]\cup[5;5+3\sqrt{2}]$
C. $[5-3\sqrt{2};2]\cup[5;5+3\sqrt{2}]$
D. $[-1;5]\cup [5+3\sqrt{2};7]$
E. $]-\infty;-1]\cup ]2;8[\cup[5+3\sqrt2;+\infty[$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 33.33%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Модультай тэгшитгэл тэнцэтгэл бишийг бодохдоо эхлээд модулийн тэмдэгээс салах шаардлагатай. Үүний тулд модулийн доторх илэрхийлэл тус бүрийг эерэг, сөрөг байх мужуудыг олж муж тус бүрт бодолт хийнэ.
Бодолт: $D\colon |x-5|-3\neq0\Rightarrow x\neq8$, $x\neq2$ байна.
$2-x=0$, $x-5=0$-ээс $2; 5$ гэсэн утгууд гарах тул эдгээр тоонуудаар тоон шулууныг хувааж $x\le 2$; $2< x\le 5$; $5< x$ гэсэн 3 мужид бодъё.
а) $x\le 2$ үед $x-5< 0$, $2-x\ge 0$ тул $\dfrac{9}{-x+5-3}\leq 2-x\Leftrightarrow \dfrac{9}{2-x}\le 2-x$. $2-x\ge 0$ ба $x\neq 2$ тул $3^3\le (2-x)^2\Rightarrow 3\le 2-x$ буюу $x\le-1$.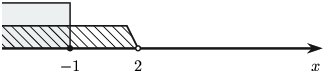
б) $2< x\le 5$ үед $x-5\le 0$, $2-x< 0$ тул $$\dfrac{9}{-x+5-3}\leq x-2\Leftrightarrow \dfrac{9}{2-x}\le x-2\Leftrightarrow\dfrac{9+(2-x)^2}{2-x}\le 0.$$ $2-x< 0$ тул $2< x\le 5$ мужийн бүх тоо шийд болно.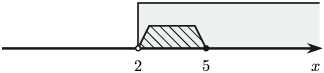
в) $5< x$ үед $x-5>0$, $2-x< 0$ тул $$\dfrac{9}{x-5-3}\le x-2\Leftrightarrow\dfrac{9}{x-8}\le x-2\Leftrightarrow$$ $$\Leftrightarrow\dfrac{9-(x-2)(x-8)}{x-8}\le 0\Leftrightarrow\dfrac{x^2-10x+7}{x-8}\ge 0$$ болно. Эндээс $x\in [5-3\sqrt2;8[\cup [5+3\sqrt2;+\infty[$ болно. $5< x$-ийг тооцвол $]5;8[\cup[5+3\sqrt2;+\infty[$.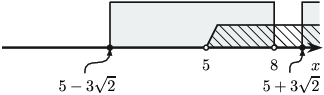
Шийдүүдээ нэгтгэвэл $]-\infty;-1]\cup ]2;8[\cup[5+3\sqrt2;+\infty[$.
$2-x=0$, $x-5=0$-ээс $2; 5$ гэсэн утгууд гарах тул эдгээр тоонуудаар тоон шулууныг хувааж $x\le 2$; $2< x\le 5$; $5< x$ гэсэн 3 мужид бодъё.
а) $x\le 2$ үед $x-5< 0$, $2-x\ge 0$ тул $\dfrac{9}{-x+5-3}\leq 2-x\Leftrightarrow \dfrac{9}{2-x}\le 2-x$. $2-x\ge 0$ ба $x\neq 2$ тул $3^3\le (2-x)^2\Rightarrow 3\le 2-x$ буюу $x\le-1$.
б) $2< x\le 5$ үед $x-5\le 0$, $2-x< 0$ тул $$\dfrac{9}{-x+5-3}\leq x-2\Leftrightarrow \dfrac{9}{2-x}\le x-2\Leftrightarrow\dfrac{9+(2-x)^2}{2-x}\le 0.$$ $2-x< 0$ тул $2< x\le 5$ мужийн бүх тоо шийд болно.
в) $5< x$ үед $x-5>0$, $2-x< 0$ тул $$\dfrac{9}{x-5-3}\le x-2\Leftrightarrow\dfrac{9}{x-8}\le x-2\Leftrightarrow$$ $$\Leftrightarrow\dfrac{9-(x-2)(x-8)}{x-8}\le 0\Leftrightarrow\dfrac{x^2-10x+7}{x-8}\ge 0$$ болно. Эндээс $x\in [5-3\sqrt2;8[\cup [5+3\sqrt2;+\infty[$ болно. $5< x$-ийг тооцвол $]5;8[\cup[5+3\sqrt2;+\infty[$.
Шийдүүдээ нэгтгэвэл $]-\infty;-1]\cup ]2;8[\cup[5+3\sqrt2;+\infty[$.