Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Муруйнуудын хоорондох өнцөг
$f(x)=\dfrac{1}{x}$ ба $g(x)=\sqrt{x}$ функцүүдийн график $A(\fbox{a},\fbox{b})$ цэгт огтлолцоно. $f(x)$ функцийн $A$ цэгт татсан шүргэгч шулууны тэгшитгэл $y=\fbox{cd}x+\fbox{e}$, $g(x)$ функцийн $A$ цэгт татсан шүргэгч шулууны тэгшитгэл $y=\dfrac{1}{\fbox{f}}x+\dfrac{1}{\fbox{g}}$ байна. Эдгээр шүргэгч шулуунуудын хоорондох хурц өнцөг нь $\arctg\fbox{h}$ байна.
ab = 11
cde = -12
fg = 22
h = 3
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 29.35%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
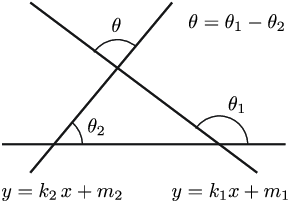
Заавар: Хоёр шулууны хоорондох өнцөг:
$$\tg\theta=\tg(\theta_1-\theta_2)=\dfrac{\tg\theta_1-\tg\theta_2}{1+\tg\theta_1\cdot\tg\theta_2}=\dfrac{k_1-k_2}{1+k_1\cdot k_2}$$
Бодолт: $f(x)=\dfrac{1}{x}$ ба $g(x)=\sqrt{x}$ функцүүдийн график $A(x,y)$ цэгт огтлолцох бол $\left\{\begin{array}{c}y=1/x\\ y=\sqrt{x}\end{array}\right.\Rightarrow x=1, y=1$. $f^\prime(x)=-\frac{1}{x^2}$ байна. $x_0=1$, $f(1)=1$,
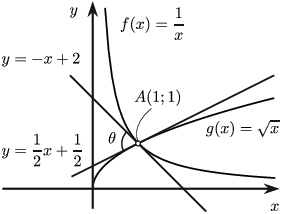
$f^\prime(1)=-\frac{1}{1^2}=-1$-ийг $$y=f^\prime(x_0)(x-x_0)+f(x_0)$$ шүргэгчийн тэгшитгэлд орлуулбал $$y=-(x-1)+1=-x+2.$$ $g^\prime(x)=\dfrac{1}{2\sqrt x}$ байна. $x_0=1$, $g(1)=1$, $g^\prime(1)=\frac{1}{2\sqrt{1}}=\frac12$-ийг $$y=g^\prime(x_0)(x-x_0)+g(x_0)$$ шүргэгчийн тэгшитгэлд орлуулбал $$y=\dfrac12(x-1)+1=\dfrac12 x+\dfrac12$$ байна. Эдгээр шүргэгч шулуунуудын хоорондох хурц өнцгийн тангенс $\tg\theta=\dfrac{\frac12-(-1)}{1+\frac12\cdot(-1)}=3$ байна. Иймд өнцөг нь $\theta=\arctg 3$ байна.
$f^\prime(1)=-\frac{1}{1^2}=-1$-ийг $$y=f^\prime(x_0)(x-x_0)+f(x_0)$$ шүргэгчийн тэгшитгэлд орлуулбал $$y=-(x-1)+1=-x+2.$$ $g^\prime(x)=\dfrac{1}{2\sqrt x}$ байна. $x_0=1$, $g(1)=1$, $g^\prime(1)=\frac{1}{2\sqrt{1}}=\frac12$-ийг $$y=g^\prime(x_0)(x-x_0)+g(x_0)$$ шүргэгчийн тэгшитгэлд орлуулбал $$y=\dfrac12(x-1)+1=\dfrac12 x+\dfrac12$$ байна. Эдгээр шүргэгч шулуунуудын хоорондох хурц өнцгийн тангенс $\tg\theta=\dfrac{\frac12-(-1)}{1+\frac12\cdot(-1)}=3$ байна. Иймд өнцөг нь $\theta=\arctg 3$ байна.