Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Бодлого №4801
$A(1;1)$, $B(2;3)$, $C(4;-2)$ цэгүүд өгөгдөв. $AB$ хэрчмийн урт $\sqrt{\fbox{a}}$, $AB$ шулууны тэгшитгэл $\fbox{b}x-\fbox{c}y-1=0$ байна. $C$ цэгээс $AB$ шулуун хүртэлх зай $\dfrac{\fbox{d}}{\sqrt{\fbox{e}}}$ бөгөөд $ABC$ гурвалжны талбай нь $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
a =5
bc =21
de =95
fg =92
Бодлогын төрөл:Нөхөх
Амжилтын хувь:16.96%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:
Бодолт: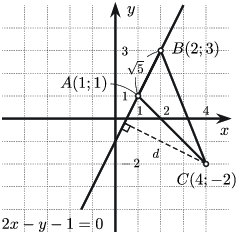
$AB=\sqrt{(2-1)^2+(3-1)^2}=\sqrt5$. $$AB\colon \dfrac{x-1}{2-1}=\dfrac{y-1}{3-1}\Rightarrow 2x-y-1=0,$$ $$d=\dfrac{|2\cdot 4-(-2)-1|}{\sqrt{2^2+(-1)^2}}=\dfrac{9}{\sqrt5}.$$ $S=\dfrac12\cdot AB\cdot d=\dfrac12\cdot\sqrt5\cdot\dfrac{9}{\sqrt5}=\dfrac{9}{2}.$
$AB=\sqrt{(2-1)^2+(3-1)^2}=\sqrt5$. $$AB\colon \dfrac{x-1}{2-1}=\dfrac{y-1}{3-1}\Rightarrow 2x-y-1=0,$$ $$d=\dfrac{|2\cdot 4-(-2)-1|}{\sqrt{2^2+(-1)^2}}=\dfrac{9}{\sqrt5}.$$ $S=\dfrac12\cdot AB\cdot d=\dfrac12\cdot\sqrt5\cdot\dfrac{9}{\sqrt5}=\dfrac{9}{2}.$
Сорилго
ЭЕШ математик №08 Огторгуйн геометр 3 Аналитик геометр вектор вектор тестийн хуулбар 2021-08-14 сорил Шулууны тэгшитгэл ААТТШ тестийн хуулбар ААТТШ тестийн хуулбар тестийн хуулбар Аналитик геометр ААТТШ ААТТШ тестийн хуулбар Математик ЭЕШ 2024-6-18