Монгол Бодлогын Сан

Заавар: $f(x)=ax^3+bx^2+cx+d$ куб олон гишүүнтийн хувьд $f'(x)=0$ тэгшитгэл $\alpha,\beta\in\mathbb R$ гэсэн ялгаатай 2 бодит шийдтэй бол $f(x)=0$ тэгшитгэл

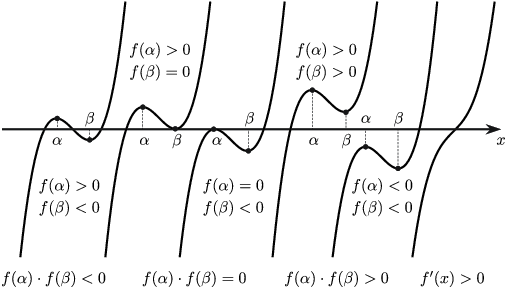
1. $f(\alpha)\cdot f(\beta)< 0$ үед 3 бодит шийдтэй.
2. $f(\alpha)\cdot f(\beta)=0$ үед 2 бодит шийдтэй.
3. $f(\alpha)\cdot f(\beta)>0$ үед 1 бодит шийдтэй.

Хэрэв $f'(x)=0$ тэгшитгэл нэг бодит шийдтэй, эсвэл огт шийдгүй бол $f(x)=0$ тэгшитгэл 1 бодит шийдтэй байна.

Бодолт: $f^\prime(x)=6x^2-18x+12=6(x-1)(x-2)$ тул $x=2$ цэгт минимум утга, $x=1$ цэг максимум утгатай байна. $f(x)=0$ тэгшитгэл 3 бодит шийдтэй $\Leftrightarrow$ $f(1)\cdot f(2)< 0$ буюу $$(2\cdot 1^3-9\cdot 1^2+12\cdot 1+p)(2\cdot 2^3-9\cdot 2^2+12\cdot 2+p)< 0\Leftrightarrow$$ $$\Leftrightarrow (5+p)(4+p)< 0$$ тул $-5< p< -4$ үед гурван шийдтэй. $x_1+x_3=2x_2$ (аримфметик прогрессийн дараалсан гишүүд) үед $(x_2,f(x_2))$ цэг нь графикийн тэгш хэмийн төв болох тул $x_2=\dfrac{1+2}{2}$. Иймд $$2\cdot1.5^3-9\cdot1.5^2+12\cdot 1.5+p=0\Rightarrow p=-4.5.$$