Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Харьцаагаар хуваах цэг
$ABCD-EFGH$ параллелепипедийн $AB$, $AD$ талуудыг $2:1$ харьцаагаар хуваах цэгүүд нь харгалзан $P$, $Q$ ба $EG$ хэрчмийг $1:2$ харьцаагаар хуваах цэг нь $R$ байв. Параллелепипедийн $AG$ диагональ $PQR$ гурвалжны хүндийн төв $K$-г дайрах бол $K$ цэг $AG$-г $\fbox{a}:\fbox{b}$ харьцаагаар хуваана. $\overrightarrow{AG}=\fbox{c}\overrightarrow{AK}$
ab = 12
c = 3
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 26.49%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\overrightarrow{AP}=\dfrac{2}{3}\overrightarrow{AB}$, $\overrightarrow{AQ}=\dfrac{2}{3}\overrightarrow{AD}$, $\overrightarrow{AR}=\overrightarrow{AE}+\dfrac{1}{3}\overrightarrow{EG}=\overrightarrow{AE}+\dfrac{\overrightarrow{AB}+\overrightarrow{AD}}{3}$.
Бодолт: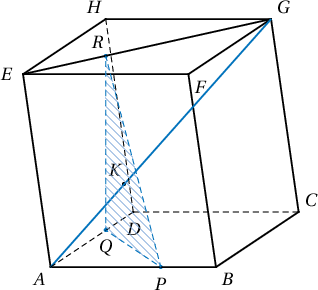 
$K$ цэг $PQR$ гурвалжны хүндийн төв тул $$\overrightarrow{AK}=\dfrac{\overrightarrow{AP}+\overrightarrow{AQ}+\overrightarrow{AR}}{3}=\dfrac{1}{3}\Big(\dfrac23\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}+\overrightarrow{AE}+\dfrac{\overrightarrow{AB}+\overrightarrow{AD}}{3}\Big)=$$ $$=\dfrac13(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AE})=\dfrac{1}{3}\overrightarrow{AG}\Rightarrow \overrightarrow{AG}=3\overrightarrow{AK}.$$ Тул $K$ цэг $AG$-г $1:2$ харьцаагаар хуваана.
Сорилго
ЭЕШ математик №10
2017-04-10
Огторгуйн геометр 2
Мэргэжлийн курс
Векторын үйлдэл, Скаляр үржвэр
Огторгуйн геометр 2 тестийн хуулбар
Мэргэжлийн курс 2021
Мэргэжлийн курс 2021
Хавтгай дахь вектор