Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Завсар дахь хамгийн бага утгын функц
$\displaystyle y=x^2-2x+3$ функцийн $t\le x\le t+2$ завсар дээрх хамгийн бага утгийг $m(t)$ гэе. $$m(t)=\left\{\begin{array}{ll} t^2+2t+3, & t< -\fbox{a} \\ 2, & -\fbox{a}\le t< \fbox{b} \\ t^2-2t+3, & \fbox{b}\le t \\ \end{array}\right.$$ болно. Иймд $-2\le t\le 5 $ үед $m(t)$-ийн хамгийн их утга $\fbox{cd}$ байна.
ab = 11
cd = 18
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 22.66%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Хамгийн бага утгаа $x=t$, $x=1$, $x=t+2$-ийн аль нэг дээр авах боломжтой.
Бодолт: $x=1$ цэг дээр функц хамгийн бага утгаа авах тул $$t\le1\le t+2$$ буюу $$-1\le t\le 1$$ үед хамгийн бага утга нь $2$ байна.
Хэрэв $t<-1$ бол $x< t+2< 1$ болох тул буурах функц байна. Иймд $x=t+2$ дээр хамгийн бага утгаа авах ба хамгийн бага утга нь $$(t+2)^2-2(t+2)+3=t^2+2t+3$$ байна.
Харин $1\le t$ үед $1\le t\le x$ тул өсөх функц байна. Иймд $x=t$ дээр хамгийн бага утгаа авах бай хамгийн бага утга нь $$t^2-2t+3$$ байна.
$m(t)$ нь $]-\infty;-1]$ завсарт буурч, $[-1;1]$ завсарт тогтмол, $[1;+\infty[$ завсарт өсөх тасралтгүй функц байна. Иймд хамгийн их утгаа мужийн захын цэгүүдийн аль нэг дээр л авах боломжтой. $m(-2)=(-2)^2+2(-2)+3=3$, $m(t)=5^2-2\cdot5+3=18$ тул $[-2;5]$ завсар дээрх хамгийн их утга нь $m(5)=18$ байна.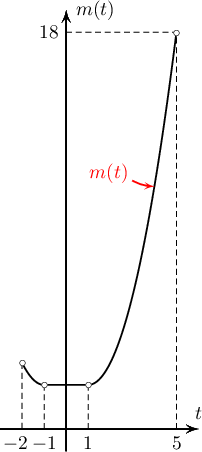
Хэрэв $t<-1$ бол $x< t+2< 1$ болох тул буурах функц байна. Иймд $x=t+2$ дээр хамгийн бага утгаа авах ба хамгийн бага утга нь $$(t+2)^2-2(t+2)+3=t^2+2t+3$$ байна.
Харин $1\le t$ үед $1\le t\le x$ тул өсөх функц байна. Иймд $x=t$ дээр хамгийн бага утгаа авах бай хамгийн бага утга нь $$t^2-2t+3$$ байна.
$m(t)$ нь $]-\infty;-1]$ завсарт буурч, $[-1;1]$ завсарт тогтмол, $[1;+\infty[$ завсарт өсөх тасралтгүй функц байна. Иймд хамгийн их утгаа мужийн захын цэгүүдийн аль нэг дээр л авах боломжтой. $m(-2)=(-2)^2+2(-2)+3=3$, $m(t)=5^2-2\cdot5+3=18$ тул $[-2;5]$ завсар дээрх хамгийн их утга нь $m(5)=18$ байна.