Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Квадратыг багтаасан тойргийн урт
$ABCD$ квадратын талын урт 3 бол түүнийг багтаасан тойргийн урт нь
A.$12\pi$ B.$4\pi\sqrt3$ C.$2\pi\sqrt{10}$ D.$6\pi\sqrt2$ E.$3\pi\sqrt2$
Бодлогын төрөл:Сонгох
Амжилтын хувь:56.90%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Квадратын диагональ нь багтаасан тойргийн диаметр болно.
Бодолт: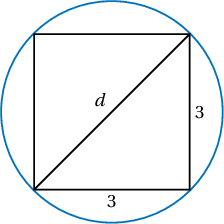
Диагоналийн урт нь $d^2=3^2+3^2$ буюу $d=\sqrt{18}=3\sqrt2$. Тойргийн уртыг диаметрт харьцуулсан харьцаа $\dfrac{\ell}{d}=\pi$ тул $\ell=3\pi\sqrt2$ байна.
Сорилго
2016-03-17 Хавтгайн геометр 1 математик113 2020-01-09 ДӨРВӨН ӨНЦӨГТ Хавтгайн геометр 1 тестийн хуулбар