Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Параболын шүргэгч
$k>0$ байг. $C\colon y=x^2$ параболын $(k, k^2)$ цэгт татсан шүргэгч шулууныг $\ell$ гэе.
- $\ell$ шулууны тэгшитгэл $y=\fbox{a}kx-k^2$ болно.
- $C$ парабол $\ell$ шулуун ба $y$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбай $S=\dfrac{k^{\fbox{b}}}{\fbox{c}}$.
- $S=72$ бол $k=\fbox{d}$ байна.
a = 2
bc = 33
d = 6
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 31.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
- $f(x)$ функцийн графикийн $(x_0,f(x_0))$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $$y=f'(x_0)(x-x_0)+f(x_0)$$ байдаг.
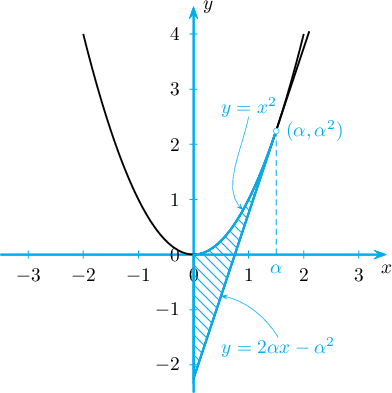
- $y=x^2$ парабол, түүний $x=\alpha>0$ цэгт татсан шүргэгч шулуун ба $x=0$ босоо шулуунаар зааглагдсан хэсгийн талбай нь:
$$S=\int\limits_{0}^{\alpha}x^2-(2\alpha x-\alpha^2) \,\mathrm{d}x=\int\limits_{0}^{\alpha}(x-\alpha)^2 \,\mathrm{d}x$$
тодорхой интегралаар илэрхийлэгдэнэ.
- Өмнөх хэсгийн томъёог ашиглан бод.
Бодолт:
- $f(x)=x^2$ параболын $(k,f(k))$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $$y=f'(k)(x-k)+f(k)=2k(x-k)+k^2=2kx^2-k^2$$ байна.
- Зааварт байгаа томъёог ашиглан бодъё. $y=x^2$ парабол, түүний $x=k$ цэгт татсан шүргэгч шулуун ба $x=0$ босоо шулуунаар зааглагдсан хэсгийн талбай нь: $$S=\int\limits_{0}^{k}(x-k)^2 \,\mathrm{d}x=\dfrac{(x-k)^3}{3}\Bigg|_0^k=\dfrac{(k-k)^3}{3}-\dfrac{(0-k)^3}{3}=\dfrac{k^3}{3}.$$
- $\dfrac{k^3}{3}=72\Rightarrow k=6$.