Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.

$A(1;1), B(-3;4), C(3;2)$ цэгүүд өгөгдөв.

a =5

bcd =347

e =2

f =5

Бодлогын төрөл:Нөхөх

Амжилтын хувь:42.81%

Бодлогыг оруулсан: baysaa41@yahoo.com

Заавар:

$(x_1;y_1), (x_2; y_2)$ цэгүүдийн хоорондох зай $$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.$$
$(x_1;y_1), (x_2; y_2)$ цэгүүдийг дайрсан шулууны тэгшитгэл нь: $$\dfrac{x-x_1}{x_2-x_2}=\dfrac{y-y_1}{y_2-y_1}.$$
$(x_0; y_0)$ цэгээс $ax+bx+c=0$ шулуун хүртэлх зай: $$\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}.$$
$(x_1;y_1), (x_2; y_2), (x_3; y_3)$ цэгүүдэд оройтой гурвалжны талбай нь: $$S=\dfrac12|x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2|.$$ Манай тохиолдолд $S=\dfrac{AB\cdot h_c}{2}$ томъёог ашиглан бодож болно.

Бодолт: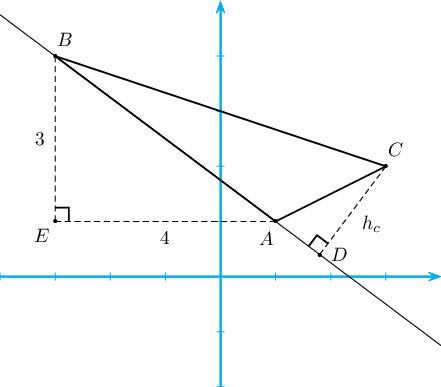

Зааварт дурдсан томъёонуудыг шууд ашиглан бодъё:

$\sqrt{(-3-1)^2+(4-1)^2}=5$.
$\dfrac{x-1}{-3-1}=\dfrac{y-1}{4-1}\Rightarrow 3x+4y-7=0$.
$\dfrac{|3\cdot 3+4\cdot 2-7|}{\sqrt{3^2+4^2}}=\dfrac{10}{5}=2$.
$AB=5$. $h_c=2$ байна. Учир нь $C$ цэгээс $AB$ шулуун хүртэлх зай нь $h$ байна. Иймд $S=\dfrac{5\cdot 2}{2}=5$.