Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Давхар тэнцэтгэл биш
$1 \le \dfrac{2-x}{x+1} \le 2$ тэнцэтгэл бишийг бод.
A. $(-\infty;0]$
B. $\left[-\dfrac{1}{3};0\right]$
C. $\left[0;\dfrac{1}{2}\right]$
D. $\left[-\dfrac{1}{2};\dfrac{1}{2}\right]$
E. $[0;+\infty[$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 73.64%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $$f(x)\le g(x)\le h(x)\Leftrightarrow\left\{\begin{array}{c} f(x)\le g(x)\\ g(x)\le h(x)\end{array}\right.$$
болохыг ашигла.
Бодолт: $$1\le \dfrac{2-x}{x+1}\le 2\Leftrightarrow\left\{\begin{array}{c} 1\le \dfrac{2-x}{x+1}\\ \dfrac{2-x}{x+1}\le 2\end{array}\right.\Leftrightarrow\left\{\begin{array}{c} 0\le \dfrac{(2-x)-(x+1)}{x+1}\\ \dfrac{2-x-2(x+1)}{x+1}\le 0\end{array}\right.$$
$$\Leftrightarrow\left\{\begin{array}{c} 0\le \dfrac{1-2x}{x+1}\\ \dfrac{-3x}{x+1}\le 0\end{array}\right.\Leftrightarrow\left\{\begin{array}{c} (x+1)\big(x-\tfrac12\big)\le 0\\ 0\le (x+1)x\\ x+1\neq0\end{array}\right.$$
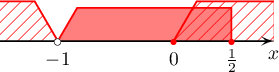тул шийд нь эдгээрийн огтлолцол буюу $\left[0;\dfrac{1}{2}\right]$ байна.