Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Параметртэй тэнцэтгэл биш
$|x+1|-|x-1|\ge a(x+1)$ тэнцэтгэл бишийг бод.
A. $\left\{\begin{array}{rl}0< a\le1 & \mbox{бол }x\in]-\infty;\frac{a}{a+2}]\cup[\frac a{a-2};\frac{a-2}a] \\a>1 & \mbox{бол }x\in]-\infty;\frac{a+2}{a}]\end{array}\right.$
B. $\left\{\begin{array}{rl}a\le0 & \mbox{бол }x\in\mathbb{R} \\0< a\le1 & \mbox{бол }x\in]-\infty;\frac{a+2}{a}]\cup[\frac a{2-a};\frac{2-a}a] \\a>1 & \mbox{бол }x\in]-\frac{a+2}a;+\infty[\end{array}\right.$
C. $\left\{\begin{array}{rl} a\le0 & \mbox{бол }x\in\mathbb{R} \\0< a\le1 & \mbox{бол }x\in]-\infty;\frac a{a+2}]\cup[\frac{2-a}a;\frac a{a-2}]\end{array}\right.$
D. $\left\{\begin{array}{rl} a\le0 & \mbox{бол }x\in[\frac{a}{2-a};+\infty[ \\ 0< a\le1 & \mbox{бол }x\in]-\infty;-\frac{a+2}{a}]\cup[\frac a{2-a};\frac{2-a}a] \\ a>1 & \mbox{бол }x\in]-\infty;-\frac{a+2}a] \end{array}\right.$
E. $x\in\left]\frac{2}{a}-1;+\infty\right[$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 42.31%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Графикийн аргаар бод.
Бодолт: $f(x)=|x+1|-|x-1|$ функцийн график ба $g(x)=a(x+1)$ функцийн графикийг $a$-ийн ялгаатай утгуудад байгуулбал:
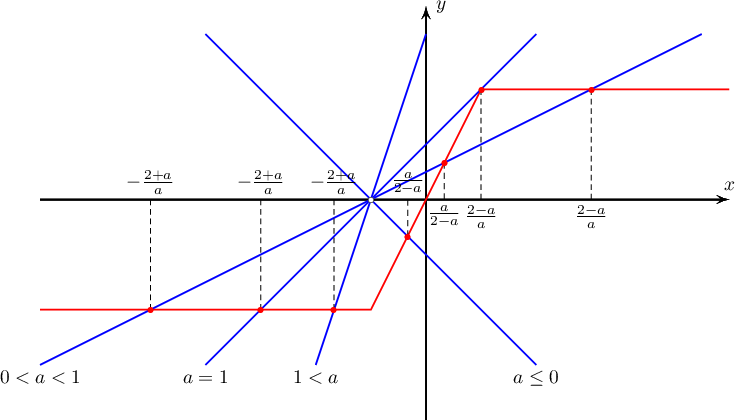$$a(x+1)=-2\Rightarrow x=-\dfrac{2}{a}-1=-\dfrac{2+a}{a}$$
$$a(x+1)=2x\Rightarrow x=\dfrac{a}{2-a}$$
$$a(x+1)=2\Rightarrow x=\dfrac{2}{a}-1=\dfrac{2-a}{a}$$
тул тэнцэтгэл бишийн шийд
$$\left\{\begin{array}{rl}
a\le0 & \mbox{бол }x\in[\frac{a}{2-a};+\infty[ \\
0< a\le1 & \mbox{бол }x\in]-\infty;-\frac{a+2}{a}]\cup[\frac a{2-a};\frac{2-a}a] \\
a>1 & \mbox{бол }x\in]-\infty;-\frac{a+2}a]
\end{array}\right.$$