Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Квадрат тэгшитгэлийн шийдийн байршил
$y=(-2m-2)x^2+(-m-1)x+2$ квадрат гурван гишүүнт $m$-ийн ямар утгуудад $x_1< 1 < x_2$ язгууртай байх вэ?
A.$]-1;0[$ B.$]-1;-\frac23[$ C.$]-1;-\frac14[$ D.$]-1;-\frac12]$ E.$]-1;-\frac13[$
Бодлогын төрөл:Сонгох
Амжилтын хувь:44.03%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
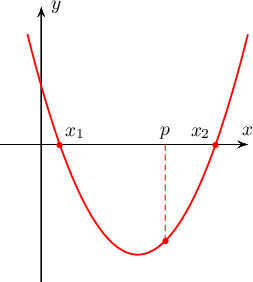
Заавар:$f(x)=x^2+bx+c$ байг. $f(x)=0$ тэгшитгэл $x_1< p$, $x_2>p$ гэсэн 2 бодит шийдтэй байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $f(p)<0$ байдаг.
Бодолт:Хоёр шийдтэй тул $-2m-2\neq0$ гэж үзэж болно. Иймд
$$(-2m-2)x^2+(-m-1)x+2=0\Leftrightarrow x^2+\dfrac{1}{2}x-\dfrac{1}{m+1}=0$$
байна. Сүүлийн тэгшитгэл $x_1< 1$, $x_2>1$ шийдтэй байхын зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь
$$1^2+\frac12\cdot 1-\dfrac{1}{m+1}<0\Leftrightarrow\dfrac{6m+2}{m+1}<0$$
тул $m\in]-1;-\frac13[$ байна.
Сорилго
2016-03-19 hw-56-2016-06-15 2016-12-14 Ном тоо тоолол Квадрат тэгшитгэл, Виетийн теорем Өмнөговь Параметртэй тэгшитгэл Параметртэй тэгшитгэл Алгебрийн тэгшитгэл - Квадрат тэгшитгэл алгебр алгебр Квадрат Тэгшитгэл, Тэнцэтгэл биш 2022-2023 хичээлийн жил