Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Модультай тэгшитгэлийн шийдийн тоо
$\sqrt{x^2-4|x|+5}=b$ тэгшитгэл
- $b< \fbox{a}$ үед шийдгүй.
- $b=\fbox{a}$ үед $x_{1,2}=\pm\fbox{b}$ гэсэн хоёр шийдтэй.
- $\fbox{a}< b< \sqrt{\fbox{c}}$ үед $x_{1,2,3,4}=\pm\left(\fbox{d}\pm\sqrt{\fbox{e}b^{\fbox{f}}+\fbox{gh}}\right)$ гэсэн 4 шийдтэй.
- $b=\sqrt{\fbox{c}}$ үед $x_{1,2}=\pm\fbox{i}, x_3=\fbox{j}$ гэсэн гурван шийдтэй.
- $b>\sqrt{\fbox{c}}$ үед $x_{1,2}=\pm\left(\fbox{d}+\sqrt{\fbox{e}b^{\fbox{f}}+\fbox{gh}}\right)$ гэсэн хоёр шийдтэй.
a = 1
b = 2
c = 5
defgh = 212-1
ij = 40
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 10.63%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $y=x^2-4|x|+5$ функцийн графикийг байгуул.
Бодолт: $b<0$ үед $\sqrt{x^2-4|x|+5}=b$ тэгшитгэл шийдгүй байна.
$b\ge 0$ үед $$\sqrt{x^2-4|x|+5}=b\Leftrightarrow x^2-4|x|+5=b^2$$ болно.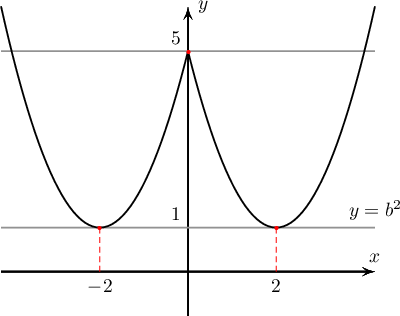
$f(x)=x^2-4|x|+5$ функцийн график, $y=b^2$ функцийн графиктай огтлолцох цэгийн тоо нь анхны тэгшитгэлийн шийдийн тоо байна. Зургаас харахад $b^2<1$ үед огтцлолцлын цэг байхгүй, $b^2=1$ буюу $b=1$ үед 2 ерөнхий цэгтэй, $1< b^2<5$ буюу $1< b<\sqrt{5}$ үед 4 огтлолцлын цэгтэй, $b^2=5$ буюу $b=\sqrt5$ үед 3 огтлолцлын цэгтэй, $\sqrt{5}< b$ үед 2 огтолцлын цэгтэй байна.
Түүнчлэн $x\ge 0$ үед $|x|=x$ ба $$x^2-4x+5-b^2=0\Rightarrow $$ $$x_{1,2}=\dfrac{4\pm\sqrt{4^2-4(5-b^2)}}{2}=2\pm\sqrt{b^2-1}$$ $x<0$ үед $|x|=-x$ ба $$x^2+4x+5-b^2=0\Rightarrow $$ $$x_{1,2}=\dfrac{-4\pm\sqrt{4^2-4(5-b^2)}}{2}=-2\pm\sqrt{b^2-1}$$ болохыг ашиглан ерөнхий шийдийг бичиж болно.
$b\ge 0$ үед $$\sqrt{x^2-4|x|+5}=b\Leftrightarrow x^2-4|x|+5=b^2$$ болно.
Түүнчлэн $x\ge 0$ үед $|x|=x$ ба $$x^2-4x+5-b^2=0\Rightarrow $$ $$x_{1,2}=\dfrac{4\pm\sqrt{4^2-4(5-b^2)}}{2}=2\pm\sqrt{b^2-1}$$ $x<0$ үед $|x|=-x$ ба $$x^2+4x+5-b^2=0\Rightarrow $$ $$x_{1,2}=\dfrac{-4\pm\sqrt{4^2-4(5-b^2)}}{2}=-2\pm\sqrt{b^2-1}$$ болохыг ашиглан ерөнхий шийдийг бичиж болно.