Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Хялбар логарифм тэнцэтгэл биш
$\log_{0.1}\left(\dfrac2{x-4}\right)\leq\log_{0.1}(7-x)$ тэнцэтгэл бишийг бод.
A.$4< x\leq5$ B.$6\leq x<7$ C.$4< x\leq5\bigcup6\leq x<7$ D.$5< x<6$ E.$4< x<7$
Бодлогын төрөл:Сонгох
Амжилтын хувь:73.85%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$y=\log_{0.1}x$ нь буурах функц тул
$$\log_{0.1}x_1<\log_{0.1}x_2\Leftrightarrow x_1>x_2>0$$
Бодолт:$$\log_{0.1}\left(\dfrac2{x-4}\right)\leq\log_{0.1}(7-x)\Leftrightarrow \dfrac{2}{x-4}\ge 7-x>0$$
болно. Иймд
$\left\{\begin{array}{c}
\dfrac{2}{x-4}\ge 7-x\\
7-x>0
\end{array}\right.$
болно.
$$\dfrac{2}{x-4}\ge 7-x\Leftrightarrow\dfrac{2-(x-4)(7-x)}{x-4}\ge 0\Leftrightarrow$$
$$\dfrac{x^2-11x+60}{x-4}=\dfrac{(x-5)(x-6)}{x-4}\ge 0$$
ба интервалын аргаар бодвол
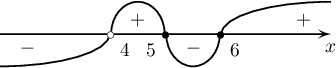$x\in]4;5]\cup[6;+\infty[$ байна.
$7-x>0$ болохыг тооцвол бодлогын шийд $$4< x\leq5\bigcup6\leq x<7$$ болно.
$7-x>0$ болохыг тооцвол бодлогын шийд $$4< x\leq5\bigcup6\leq x<7$$ болно.