Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №6811
$\log_{\sin x}(1+\cos 2x+\cos 4x)=0$ тэгшитгэлийг бод.
A. $\dfrac{\pi}{6}+2\pi k, -\dfrac{\pi}{2}+2\pi n$
B. $\dfrac{\pi}{3}+2\pi k, \dfrac{5\pi}{6}+2\pi n$
C. $-\dfrac{\pi}{6}+\pi k$
D. $\pm\dfrac{\pi}{3}+2\pi k$
E. $(-1)^k\dfrac{\pi}{6}+\pi k$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 51.92%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Логарифмын тодорхойлолт ёсоор:
$$\log_{\sin x}(1+\cos 2x+\cos 4x)=0\Leftrightarrow\left\{\begin{array}{c}
0<\sin x<1\\
\cos2x+\cos4x=0
\end{array}\right.$$
Бодолт: Нийлбэрийг үржвэрт хувиргах томьёо ашиглавал
$$\cos2x+\cos4x=2\cos\dfrac{2x+4x}{2}\cos\dfrac{2x-4x}{2}=0$$
тул $\cos x=0$ эсвэл $\cos3x=0$ болно. $\cos x=0$ үед $\sin x=\pm1$ тул $0<\sin x<1$ нөхцөлд тохирохгүй.
$$\cos 3x=0\Leftrightarrow 3x=\dfrac{\pi}{2}+\pi k\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{\pi k}{3}$$
Эдгээрийг тригонометрийн нэгж тойрог дээр дүрсэлбэл
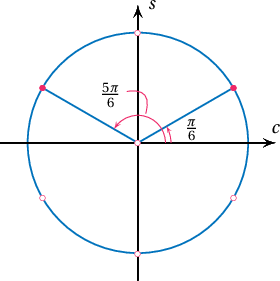болох ба эдгээрээс зөвхөн $\dfrac{\pi}{6}$, $\dfrac{5\pi}{6}$ өнцгүүд дээр синусийн утга нь $]0;1[$ засварт байх тул тэгшитгэлийн ерөнхий шийд нь $$x=(-1)^k\dfrac{\pi}{6}+\pi k$$
байна.
Сорилго
Алгебр сэдвийн давтлага 1
Тригонометрийн тэгшитгэл Нийлбэрийг үржвэрт хувиргах томъёо хэрэглэх
Алгебр сэдвийн давтлага 1
Алгебр сэдвийн давтлага 1 тестийн хуулбар