Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
$\sin162^\circ$
$\sin 162^{\circ}=\dfrac{\sqrt{\fbox{a}}-\fbox{b}}{\fbox{c}}$.
abc = 514
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 33.33%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $162^\circ=180^\circ-18^\circ\Rightarrow\sin162^\circ=\sin 18^\circ=\cos 72^\circ$. Цааш нь $36^\circ$, $72^\circ$, $72^\circ$ өнцгүүдтэй адил хажуут гурвалжны суурийн аль нэг өнцгөөс биссектрис татаад бод.
Бодолт: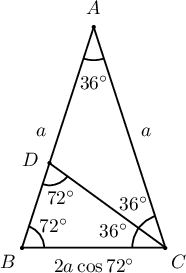 
$\angle A=36^\circ$, $\angle B=\angle C=72^\circ$ байх адил хажуут гурвалжны $AB=AC=a$ гэвэл $BC=2a\cos72^\circ$ байна. $\triangle BCD$, $\triangle CDA$ гурвалжны суурийн өнцгүүд тэнцүү тул адил хажуут байна. Иймд $$AD=DC=BC=2a\cos72^\circ$$ ба
$$BD=a-2a\cos72^\circ=2(2a\cos72^\circ)\cos72^\circ$$
тул
$$4\cos^272^\circ+2\cos72^\circ-1=0$$
$4c^2+2c-1=0$ тэгшитгэлээс $$c_{1,2}=\dfrac{-2\pm\sqrt{2^2-4\cdot4\cdot(-1)}}{8}=\dfrac{-1\pm\sqrt{5}}{4}$$
ба $\cos72^\circ>0$ тул $\cos72^\circ=\dfrac{\sqrt5-1}{4}$ байна.