Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тригонометр функцийн тодорхойлогдох муж, тэгшитгэл
$y=\log_{\sqrt{2}\cos 2x}\left(1+\sin 2x\right)-2$ функц өгөгдөв.
- Функцийн тодорхойлогдох муж $ \left\{ % \begin{array}{l} x\ne -\dfrac{\fbox{a}}{\fbox{b}}\pi+\fbox{c}\pi k \\ n\pi-\dfrac{\pi}{\fbox{d}}< x< \dfrac{\pi}{\fbox{e}}+n\pi \\ \end{array} % \right. k,n\in \mathbb Z.$
- $y=0$ тэгшитгэлийг бодвол $x=(-1)^n\dfrac{\pi}{\fbox{fg}}+\dfrac{n\pi }{\fbox{h}}, k,n\in \mathbb Z$
abc = 181
de = 44
fgh = 122
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 34.59%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\log_{f(x)}g(x)$ илэрхийлэл нь $f(x)>0$, $f(x)\neq1$, $g(x)>0$ үед тодорхойлогдоно.
Бодолт:
- Логарифм функцийн тодорхойлолт ёсоор $$\left\{\begin{array}{c}\sqrt2\cos 2x>0,\\ \sqrt2\cos 2x\neq1,\\1+\sin 2x>0\end{array}\right.$$ байна. $\alpha=2x$ гэвэл $\alpha$ нь
$\alpha\neq\pm\dfrac{\pi}{4}+2\pi k$, $-\dfrac{\pi}{2}+2\pi n< \alpha< \dfrac{\pi}{2}+2\pi n$ тул $$x\neq\pm\dfrac{\pi}{8}+\pi k,\ \pi n-\dfrac{\pi}{4}< x<\pi n+\dfrac{\pi}{4}$$
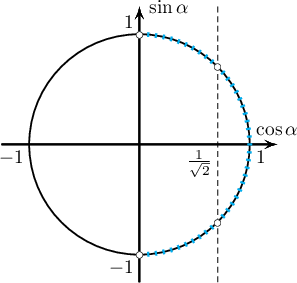
- $\log_{\sqrt{2}\cos 2x}\left(1+\sin 2x\right)-2=0\Rightarrow (\sqrt2\cos2x)^2=1+\sin 2x\Leftrightarrow 2\cos^22x=1+\sin 2x$ тул $$2(1-\sin^22x)=1+\sin 2x\Leftrightarrow2\sin^22x+\sin 2x-1=0$$ буюу $\sin2x=-1$, $\sin 2x=\dfrac12$ болно. Тодорхойлогдох мужид $\sin 2x+1>0$ тул $\sin 2x=\dfrac12$ гэсэн боломж үлдэж байна. Эндээс $2x=(-1)^n\dfrac{\pi}{6}+n\pi \Leftrightarrow x=(-1)^n\dfrac{\pi}{12}+\dfrac{n\pi}{2}$ байна.