Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Нөхцөлт магадлал
Улаан уутанд 6 улаан, 4 цагаан, хөх уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A.$\dfrac{13}{60}$ B.$\dfrac{5}{12}$ C.$\dfrac{3}{20}$ D.$\dfrac{19}{60}$ E.$\dfrac{19}{30}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:58.02%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$A$ улаан уутнаас 2 бөмбөг авах үзэгдэл, $B$ хөх уутнаас 2 бөмбөг авах үзэгдэл. $X$ нь гарч ирсэн хоёр бөмбөг хоёулаа цагаан байх үзэгдэл гэвэл
$$P(X)=P(XA)+P(XB)$$
байна. Энд $P(AB)=P(A|B)\cdot{P(B)}$ нөхцөлт магадлал ашиглан бод.
Бодолт:$P(A)=P(B)=\dfrac12$, $P(X|A)=\dfrac{C_{4}^2}{C_{10}^2}$, $P(X|B)=\dfrac{C_3^2}{C_5^2}$ тул
\begin{align*}
P(X)&=P(XA)+P(XB)\\
&=P(X|A)\cdot P(A)+P(X|B)\cdot P(B)\\
&=\dfrac{2}{15}\cdot\dfrac12+\dfrac{3}{10}\cdot\dfrac12=\dfrac{13}{60}
\end{align*}
Заавар:Модны схем ашиглаж бод.
Бодолт: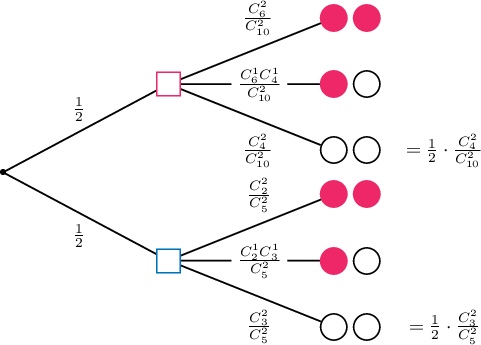
Бидний олох магадлал нь
$$\frac12\cdot\frac{C_4^2}{C_{10}^2}+\frac12\cdot\frac{C_3^2}{C_{5}^2}=\dfrac12\cdot\dfrac{6}{45}+\dfrac12\cdot\dfrac{3}{10}=\dfrac{1}{15}+\dfrac{3}{20}=\dfrac{13}{60}$$
байна.
Сорилго
2017-12-27 2017-01-13 hw-14-2017-09-01 Магадлал Сорилго 2019 №1А Магадлал, статистикийн нэмэлт 2 Нөхцөлт магадлал ба гүйцэд магадлал Магадлал, статистикийн нэмэлт 2 тестийн хуулбар Magadlal 12