Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Геометр магадлал
$[0,1]$ хэрчмээс санамсаргүйгээр $a$ ба $b$ хоёр тоог сонгоход $x^{2}+ax+b=0$ тэгшитгэл бодит шийдтэй байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ байна.
abc = 112
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 8.93%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Квадрат тэгшитгэл нь $D<0$ үед шийдгүй өөрөөр хэлбэл $D=a^2-4b<0$ байна. $Oab$ хавтгайд $0\le a,b\le 1$ квадрат дотор координатууд нь $a^2-4b<0$ нөхцөлийг хангах цэгүүдээс бүрдэх дүрсийн талбайг олж геометр магадлалын тодорхойлолт ашигла.
$M$ нь ямар нэг $X$ олонлог дээр тодорхойлогдсон хэмжээ (хэрчмийн урт, талбай, эзлэхүүн гэх мэт) байг. $Y\subseteq X$ олонлогийн хувьд геометр магадлалыг $P(Y)=\dfrac{M(Y)}{M(X)}$ гэж тодорхойлдог.
$M$ нь ямар нэг $X$ олонлог дээр тодорхойлогдсон хэмжээ (хэрчмийн урт, талбай, эзлэхүүн гэх мэт) байг. $Y\subseteq X$ олонлогийн хувьд геометр магадлалыг $P(Y)=\dfrac{M(Y)}{M(X)}$ гэж тодорхойлдог.
Бодолт: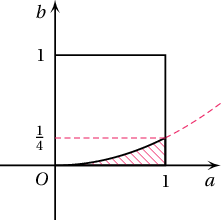 
$a^2-4b<0$ байх дүрсийн талбай нь $S=\displaystyle\int_0^1\dfrac{a^2}{4} \mathrm{d}a$ интегралаар бодогдох тул $S=\dfrac{a^3}{12}\bigg|_0^1=\dfrac{1^3}{12}-\dfrac{0^3}{12}=\dfrac{1}{12}$ болно. Энэ хэсгийн талбай нь нэгж квадратын талбайн $\dfrac{1}{12}$ хэсэг тул квадратаас санамсаргүйгээр сонгосон цэг $a^2-4b<0$ нөхцөлийг хангаж байх магадлал нь $\dfrac1{12}$ байна.