Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Гурвалжны дотор орших цэг
Гурвалжны дотор орших цэгээс талууд хүртэлх зайг, тэр талд буусан өндөрт харьцуулсан харьцааны нийлбэр хэд байх вэ?
A. $1$
B. $\dfrac13$
C. $\dfrac23$
D. $\dfrac12$
E. гурвалжны хэлбэрээс хамаарна
Бодлогын төрөл: Сонгох
Амжилтын хувь: 12.50%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: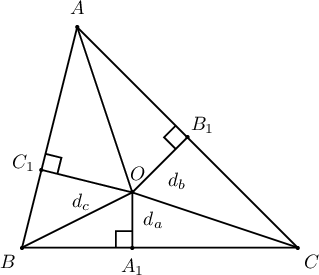 
$$S=S_{\triangle ABO}+S_{\triangle BCO}+S_{\triangle CAO}=$$
$$=\dfrac12AB\cdot d_c+\dfrac12BC\cdot d_a+\dfrac12CA\cdot d_b$$
Бодолт: Зааварт өгсөн томьёо ёсоор $\triangle ABC$-ийн дотор орших дурын $O$ цэгийн хувьд
$$S=\dfrac12AB\cdot d_c+\dfrac12BC\cdot d_a+\dfrac12CA\cdot d_b$$
томьёо биелэнэ. Энд $d_a$, $d_b$, $d_c$ нь харгалзан $O$ цэгээс $BC$, $CA$, $AB$ талууд хүртэлх зайнууд. Нөгөө талаас
$$S=\dfrac{1}{2}ABh_c=\dfrac{1}{2}BCh_a=\dfrac{1}{2}CAh_b$$
тул
$$\dfrac12AB=\dfrac{S}{h_c},~\dfrac12BC=\dfrac{S}{h_a},~\dfrac12CA=\dfrac{S}{h_b}$$
байна. Үүнийг эхний илэрхийлэлд орлуулбал
$$S=\dfrac{Sd_c}{h_c}+\dfrac{Sd_a}{h_a}+\dfrac{Sd_b}{h_b}\Rightarrow\dfrac{d_a}{h_a}+\dfrac{d_b}{h_b}+\dfrac{d_c}{h_c}=1$$
байна.