Монгол Бодлогын Сан

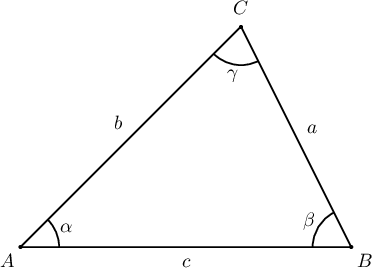
Заавар:Косинусын теоремоор $$a^2=b^2+c^2-2bc\cos\alpha\Rightarrow\cos\alpha=\dfrac{b^2+c^2-a^2}{2bc}$$ байна.

Бодолт: 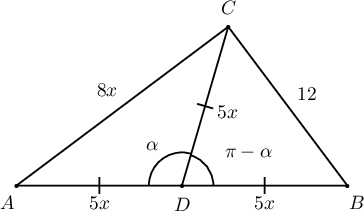2 дахь гурвалжны суурийн уртыг $8x$ гэвэл хажуу талын урт нь $5x$ байна. Энэ гурвалжны оройн өнцгийг $\alpha$ гэвэл косинусын теоремоор $$\cos\alpha=\dfrac{(5x)^2+(5x)^2-(8x)^2}{2\cdot 5x\cdot 5x}=\dfrac{-14x^2}{50x^2}=-\dfrac{7}{25}$$ Нөгөө гурвалжны оройн өнцөг нь $\pi-\alpha$ ба $$\cos(\pi-\alpha)=-\cos\alpha=\dfrac{7}{25}$$ тул косинусын теоремоор $$12^2=(5x)^2+(5x)^2-2\cdot 5x\cdot 5x\cdot\dfrac{7}{25}=36x^2$$ тул $x=2$ тул гурвалжны талууд нь $8\cdot 2=16$, $5\cdot 2=10$ байна.